dataset
We'll work on the normalized version of the trees db
-
download the sql backup from https://skatai.com/assets/db/treesdb_v03_normalized.sql
-
restore the database
from the terminal
psql -d postgres -f <path to the sql backup>/treesdb_v03_normalized.sql
or within a PSQL session
\i <path to the sql backup>/treesdb_v03_normalized.sql
This will create a new database called treesdb_v03_normalized
Explore
Check out the tables, make a few queries to get a sense of the data.
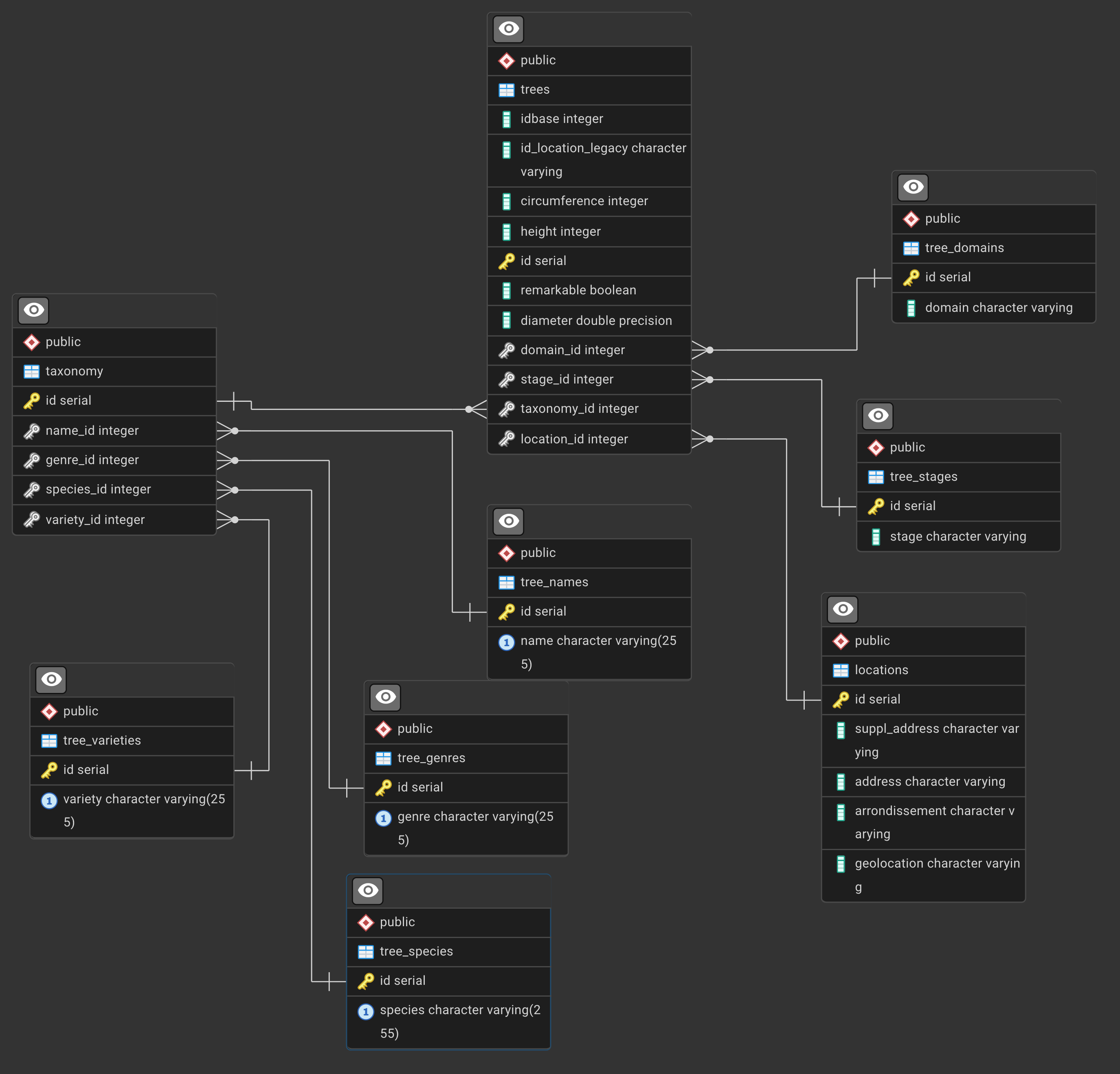
The ERD is
PostgreSQL Window Functions Exercises: Paris Trees Database
This comprehensive series of exercises will help you master window functions in PostgreSQL using a real-world dataset of trees in Paris.
important: all results are obtained after ordering by random() and limiting to a few rows. all your queries should also be ordered by random() and limited to a few rows.
Exercise 1: Basic Window Functions - Tree Count by Arrondissement
Goal: For each tree, show its arrondissement and the total count of trees in that arrondissement.
Concepts: Basic COUNT() window function with OVER(PARTITION BY)
Step-by-step guide:
- Start with the main
treestable - Join with
locationsto get arrondissement information - Use
COUNT(*) OVER (PARTITION BY arrondissement)to count trees per arrondissement - Select the tree id, arrondissement, and the count
Hints:
- Window functions don't reduce rows like
GROUP BYdoes - Each tree row will show the total count for its arrondissement
- The
PARTITION BYclause divides the data into groups for the window function
For comparison - GROUP BY approach:
SELECT
l.arrondissement,
COUNT(*) as tree_count
FROM trees t
JOIN locations l ON t.location_id = l.id
WHERE l.arrondissement IS NOT NULL
GROUP BY l.arrondissement
ORDER BY tree_count DESC;
results
id | arrondissement | trees_in_arrondissement
--------+-------------------+-------------------------
108631 | PARIS 16E ARRDT | 17128
208989 | PARIS 1ER ARRDT | 1645
18713 | PARIS 13E ARRDT | 17462
159547 | PARIS 19E ARRDT | 15235
Exercise 2: Finding the Tallest Tree per Arrondissement
Goal: For each tree, show how its height compares to the maximum height in its arrondissement.
Concepts: MAX() window function, comparing values to aggregates
Step-by-step guide:
- Join
treesandlocationstables - Use
MAX(height) OVER (PARTITION BY arrondissement)to find the tallest tree per area - Calculate the difference between each tree's height and the maximum
- Filter to only show trees with valid heights
Hints:
- You can use multiple columns in your SELECT with window functions
- Consider what
height - MAX(height) OVER (...)tells you - Trees with a difference of 0 are the tallest in their arrondissement
to get a better view of the results, you can limit the number of rows returned and order by random()
ORDER BY random() <other order by> limit 20;
results
id | arrondissement | height | max_height_in_area | diff_from_max
--------+-------------------+--------+--------------------+---------------
5422 | PARIS 11E ARRDT | 35 | 35 | 0
133998 | PARIS 20E ARRDT | 15 | 30 | -15
61004 | BOIS DE VINCENNES | 10 | 120 | -110
86518 | PARIS 20E ARRDT | 12 | 30 | -18
Exercise 3: Data Quality - Missing Heights by Genre
Here's the corrected query for Exercise 3:
Exercise 3: Data Quality - Missing Heights by Genre
Goal: Identify genres with missing height data by showing the count and percentage of trees with missing (0) heights.
Concepts: COUNT() with conditions, calculating percentages with window functions
Step-by-step guide:
- Join trees with taxonomy and tree_genres tables
- Use
COUNT(*) OVER (PARTITION BY genre)for total trees per genre - Use
COUNT(CASE WHEN height > 0 THEN 1 END) OVER (PARTITION BY genre)for trees with valid heights - Calculate the difference to find missing values (height = 0)
- Compute percentage of missing data
Hints:
- In this dataset, missing heights are stored as 0, not NULL
COUNT(CASE WHEN height > 0 THEN 1 END)only counts trees with actual height valuesCOUNT(*)counts all rows- The difference gives you the count of missing/zero heights
- Use
DISTINCTin the outer query to avoid repeated calculations
Alternative approach (more explicit):
SELECT DISTINCT
tg.genre,
COUNT(*) OVER (PARTITION BY tg.genre) as total_trees,
COUNT(*) OVER (PARTITION BY tg.genre) - COUNT(CASE WHEN t.height = 0 THEN 1 END) OVER (PARTITION BY tg.genre) as trees_with_height,
COUNT(CASE WHEN t.height = 0 THEN 1 END) OVER (PARTITION BY tg.genre) as missing_height,
ROUND(100.0 * COUNT(CASE WHEN t.height = 0 THEN 1 END) OVER (PARTITION BY tg.genre) /
COUNT(*) OVER (PARTITION BY tg.genre), 2) as pct_missing
FROM trees t
JOIN taxonomy tx ON t.taxonomy_id = tx.id
JOIN tree_genres tg ON tx.genre_id = tg.id
ORDER BY pct_missing DESC;
results
genre | total_trees | trees_with_height | missing_height | pct_missing
-------------------+-------------+-------------------+----------------+-------------
Rhododendron | 8 | 0 | 8 | 100.00
Podocarpus | 2 | 0 | 2 | 100.00
Tsuga | 1 | 0 | 1 | 100.00
Cephalotaxus | 1 | 0 | 1 | 100.00
Juniperus | 5 | 0 | 5 | 100.00
Cercidiphyllum | 8 | 1 | 7 | 87.50
Note: a SQL query with
GROUP BYwould be simpler,
For instance
SELECT
tg.genre,
COUNT(*) as total_trees,
COUNT(CASE WHEN t.height > 0 THEN 1 END) as trees_with_height,
COUNT(CASE WHEN t.height = 0 THEN 1 END) as missing_height,
ROUND(100.0 * COUNT(CASE WHEN t.height = 0 THEN 1 END) / COUNT(*), 2) as pct_missing
FROM trees t
JOIN taxonomy tx ON t.taxonomy_id = tx.id
JOIN tree_genres tg ON tx.genre_id = tg.id
GROUP BY tg.genre
ORDER BY pct_missing DESC;
Exercise 4: ROW_NUMBER - Ranking Trees by Height within Each Domain
Goal: Assign a sequential ranking to trees by height within each domain.
Concepts: ROW_NUMBER(), ordering within partitions
Step-by-step guide:
- Join trees with tree_domains
- Use
ROW_NUMBER() OVER (PARTITION BY domain ORDER BY height DESC) - Filter for trees that have height values
- Show only the top 5 trees per domain
Hints:
ROW_NUMBER()always gives unique sequential numbers (1, 2, 3, ...)- Use a subquery to filter by row_number (you can't use window functions in WHERE directly)
ORDER BY height DESCputs tallest trees first
Query Skeleton:
SELECT * FROM (
SELECT
...,
ROW_NUMBER() OVER (...) as rn
FROM ...
WHERE ...
) subquery
WHERE rn <= 5;
results
id | domain | height | height_rank
--------+--------------+--------+-------------
172122 | Alignement | 2524 | 1
152402 | Alignement | 2019 | 2
166842 | Alignement | 720 | 3
168045 | Alignement | 225 | 4
93247 | Alignement | 200 | 5
88686 | CIMETIERE | 119 | 1
91418 | CIMETIERE | 116 | 2
91576 | CIMETIERE | 35 | 3
Exercise 5: RANK vs DENSE_RANK - Handling Ties in Circumference
Goal: Compare RANK() and DENSE_RANK() behavior when trees have the same circumference within each arrondissement.
Concepts: RANK(), DENSE_RANK(), understanding ties
Step-by-step guide:
- Join trees with locations
- Apply both
RANK()andDENSE_RANK()with the same ordering - Order by circumference descending within each arrondissement
- Show the difference between the two ranking methods
Hints:
RANK()leaves gaps after ties: 1, 2, 2, 4, 5DENSE_RANK()has no gaps: 1, 2, 2, 3, 4- Look for trees with the same circumference to see the difference
- Limit results to make patterns visible
Exercise 6: Detecting Outliers - Heights Beyond 2 Standard Deviations
Goal: Identify unusually tall or short trees by comparing them to statistical measures within their species.
Concepts: AVG(), STDDEV() window functions, statistical outlier detection
Step-by-step guide:
- Join trees, taxonomy, and tree_species tables
- Calculate
AVG(height)andSTDDEV(height)per species using window functions - Compute z-score:
(height - avg) / stddev - Filter for trees where absolute z-score > 2
- Use a subquery since you need to filter on calculated window function results
Hints:
- A z-score shows how many standard deviations a value is from the mean
- Z-score > 2 or < -2 typically indicates an outlier
ABS()function gets absolute value- Only include species with enough trees for meaningful statistics
Query Skeleton:
SELECT * FROM (
SELECT
...,
AVG(...) OVER (PARTITION BY ...) as avg_height,
STDDEV(...) OVER (PARTITION BY ...) as stddev_height,
(height - AVG(...) OVER (...)) / STDDEV(...) OVER (...) as z_score
FROM ...
WHERE ...
) stats
WHERE ABS(z_score) > 2
AND stddev_height IS NOT NULL;
Exercise 7: Distribution Analysis - Percentile Ranks for Tree Diameter
Goal: Calculate what percentage of trees in each domain have a smaller diameter than each tree.
Concepts: PERCENT_RANK(), CUME_DIST(), understanding percentiles
Step-by-step guide:
- Join trees with tree_domains
- Use
PERCENT_RANK()to get relative rank (0 to 1) - Use
CUME_DIST()to get cumulative distribution - Convert to percentages for easier interpretation
- Filter for valid diameter and domain values
Hints:
PERCENT_RANK()returns 0 for the smallest value, 1 for the largestCUME_DIST()returns the fraction of rows <= current row- Multiply by 100 to convert to percentages
- These help you understand distribution within groups
Exercise 8: Multi-Level Ranking - Best Trees by Species within Each Arrondissement
Goal: Create a two-level ranking showing the tallest trees of each species within each arrondissement.
Concepts: Multiple window functions, complex partitioning
Step-by-step guide:
- Join trees, locations, taxonomy, and tree_species
- Create a ranking by height within each (arrondissement, species) combination
- Also show how this tree ranks across all species in that arrondissement
- Filter to show only top 3 per species per arrondissement
- Use subquery to filter on window function results
Hints:
- You can have multiple
OVER()clauses with differentPARTITION BYconditions - First partition:
PARTITION BY arrondissement, species - Second partition:
PARTITION BY arrondissement - This shows both local (within species) and global (within area) rankings
Query Skeleton:
SELECT * FROM (
SELECT
...,
ROW_NUMBER() OVER (PARTITION BY arr, species ORDER BY height DESC) as rank_in_species,
ROW_NUMBER() OVER (PARTITION BY arr ORDER BY height DESC) as rank_in_area
FROM ...
JOIN ... ON ...
WHERE ...
) ranked
WHERE rank_in_species <= 3;
Exercise 9: Data Quality - Identifying Imbalanced Remarkable Trees
Goal: Analyze the distribution of the remarkable flag, showing how imbalanced it is across different domains and stages.
Concepts: Conditional aggregation with window functions, handling boolean/NULL values
Step-by-step guide:
- Join trees with tree_domains and tree_stages
- Count total trees per domain/stage combination
- Count trees where
remarkable = true - Count trees where
remarkable IS NULL - Calculate percentages for each category
- Use
DISTINCTto avoid row repetition
Hints:
COUNT(CASE WHEN remarkable = true THEN 1 END)counts only TRUE valuesCOUNT(CASE WHEN remarkable IS NULL THEN 1 END)counts NULLs- Window functions with CASE statements are powerful for conditional counting
- This reveals data quality issues with the remarkable flag
Query Skeleton:
SELECT DISTINCT
domain,
stage,
COUNT(*) OVER (PARTITION BY ...) as total,
COUNT(CASE WHEN ... THEN 1 END) OVER (PARTITION BY ...) as remarkable_count,
COUNT(CASE WHEN ... IS NULL THEN 1 END) OVER (PARTITION BY ...) as null_count,
-- percentages
FROM ...
ORDER BY ...;
Exercise 10: Running Totals - Cumulative Tree Count by Circumference Range
Goal: Create a running total showing how many trees exist at or below each circumference threshold within each genus.
Concepts: SUM() with window frames, running totals, ROWS BETWEEN
Step-by-step guide:
- Join trees, taxonomy, and tree_genres
- Order trees by circumference within each genus
- Use
SUM(1) OVER (PARTITION BY genus ORDER BY circumference ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) - This creates a running count
- Round circumferences to groups (e.g., multiples of 10) for clearer analysis
Hints:
- Window frames control which rows are included in the calculation
ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROWmeans "from start to here"- This is useful for cumulative distributions
SUM(1)is the same asCOUNT(*)
Query Skeleton:
SELECT
...,
SUM(1) OVER (PARTITION BY ...
ORDER BY ...
ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) as running_total
FROM ...
WHERE ...
ORDER BY ...;
Exercise 11: Advanced - LAG and LEAD for Comparing Adjacent Trees
Goal: For trees ordered by height within each species, compare each tree to the previous and next tree.
Concepts: LAG(), LEAD(), accessing adjacent rows
Step-by-step guide:
- Join trees, taxonomy, and tree_species
- Use
LAG(height) OVER (PARTITION BY species ORDER BY height)to get previous tree's height - Use
LEAD(height) OVER (PARTITION BY species ORDER BY height)to get next tree's height - Calculate differences to see gaps in the distribution
- Filter to show interesting cases (large gaps)
Hints:
LAG(column, offset)looks backoffsetrows (default is 1)LEAD(column, offset)looks forwardoffsetrows- These return NULL at boundaries (first/last rows)
- Useful for identifying unusual gaps in sequential data
Exercise 12: Complex Analysis - Identifying Stage Distribution Anomalies
Goal: Analyze the confusing stage labels by showing how stage distribution varies across domains and highlighting unusual patterns.
Concepts: Multiple window functions, conditional logic, complex filtering
Step-by-step guide:
- Join trees with tree_stages and tree_domains
- Calculate total trees per domain
- Calculate trees per stage within each domain
- Calculate percentage distribution
- Show which stages appear in which domains
- Use window functions to identify domains with unusual stage distributions
Hints:
- Stage values are inconsistent: "adult", "young", "young & adult", and NULLs
- This exercise helps identify data quality issues
- Multiple PARTITION BY clauses can show different perspectives
- DISTINCT helps when showing summary statistics
Query Skeleton:
SELECT DISTINCT
domain,
stage,
COUNT(*) OVER (PARTITION BY domain, stage) as count_domain_stage,
COUNT(*) OVER (PARTITION BY domain) as count_domain,
COUNT(*) OVER (PARTITION BY stage) as count_stage,
-- percentages and other metrics
FROM ...
ORDER BY ...;
Exercise 13: Master Challenge - Top Varieties with Complete Statistics
Goal: For each arrondissement, find the top 3 most common tree varieties and provide comprehensive statistics including rankings, percentages, and comparisons.
Concepts: Everything combined - multiple window functions, rankings, aggregations, complex joins
Step-by-step guide:
- Join all necessary tables: trees, locations, taxonomy, tree_varieties
- Count trees per variety per arrondissement
- Rank varieties within each arrondissement by count
- Calculate statistics: avg height, max circumference, etc.
- Calculate what percentage of the arrondissement's trees each variety represents
- Filter to top 3 varieties per arrondissement
- Use subquery structure to handle complex filtering
Hints:
- This combines multiple concepts from previous exercises
- Use
DENSE_RANK()to handle ties appropriately - Multiple window functions with different PARTITION BY clauses
- Think about what statistics would be most useful for each variety
Query Skeleton:
SELECT * FROM (
SELECT
arrondissement,
variety,
COUNT(*) OVER (PARTITION BY arrondissement, variety) as variety_count,
DENSE_RANK() OVER (PARTITION BY arrondissement ORDER BY COUNT(*) OVER (PARTITION BY arrondissement, variety) DESC) as variety_rank,
AVG(...) OVER (PARTITION BY arrondissement, variety) as avg_stat,
COUNT(*) OVER (PARTITION BY arrondissement) as total_in_arrond,
-- more statistics
FROM trees t
JOIN ... ON ...
WHERE ...
) ranked_varieties
WHERE variety_rank <= 3
ORDER BY ...;
Bonus Exercise 14: NTILE - Dividing Trees into Height Quartiles
Goal: Divide trees within each genus into 4 equal groups (quartiles) based on height to understand distribution.
Concepts: NTILE(), quantile analysis
Step-by-step guide:
- Join trees, taxonomy, and tree_genres
- Use
NTILE(4)to divide trees into 4 groups - Show which quartile each tree belongs to
- Calculate statistics for each quartile
Hints:
NTILE(n)divides rows into n approximately equal groups- Returns values 1, 2, 3, 4 for quartiles
- Useful for analyzing distribution across ranges
- Can use with different values: NTILE(10) for deciles, NTILE(100) for percentiles
Summary of Window Functions Covered
- Aggregate functions:
COUNT(),SUM(),AVG(),MAX(),MIN(),STDDEV() - Ranking functions:
ROW_NUMBER(),RANK(),DENSE_RANK(),NTILE() - Distribution functions:
PERCENT_RANK(),CUME_DIST() - Offset functions:
LAG(),LEAD() - Conditional aggregation:
COUNT(CASE WHEN ... END) - Window frames:
ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW