Machine Learning

programme

supervisé vs non supervisé vs semi-supervisé
classification vs régression
calcul de sqrt(2) - Methode babylonienne de Heron
- erreur
- fonction de coût
régression linéaire
régression logistique, fonction logit

stochastic gradient descent
- gradient descent
- learning rate
- batch
overfitting
- regularisation, contrainte sur fct de cout, L1, L2
concepts machine learning
- bias-variance tradeoff
- no free lunch
- curse of dimensionality
- greedy algorithms

Notebooks

Google Colab

TP / TD

Optimiser un Gradient stochastic sur dataset UCI

normalisation des données
réglage du learning rate
réglage du batch size

Why ML ? What is ML ?

Prediction vs Modelisation

modelisation statistique :

comprendre la relation entre les variables
utilise toutes les données

prediction :

prédire des valeurs par le biais d'un modèle entrainée sur un jeux de données.
machine learning : (supervisé) utilise une partie des données pour entrainer un modele,
- split test / train / validation
question d'interprétabilité, modèles black box

Leo Breiman

Statistical Modeling the two cultures (2001)

There are two cultures in the use of statistical modeling to reach conclusions from data.

One assumes that the data are generated by a given stochastic data model. The other uses algorithmic models and treats the data mechanism as unknown.

The statistical community has been committed to the almost exclusive use of data models. This commitment has led to irrelevant theory, questionable conclusions, and has kept statisticians from working on a large range of interesting current problems.

Algorithmic modeling, both in theory and practice, has developed rapidly in fields outside statistics. It can be used both on large complex data sets and as a more accurate and informative alternative to data modeling on smaller data sets.

If our goal as a field is to use data to solve problems, then we need to move away from exclusive dependence on data models and adopt a more diverse set of tools

data, data, data

data = observations + variables
multimodale : tabulaire, texte (NLP), image, audio, vidéo, capteurs, séries temporelles

Iris, le dataset, 1936

150 samples
4 features
3 classes One class is linearly separable from the other 2; the latter are not linearly separable from each other.

Données brutes

Dans le monde réel, les données sont souvent mal foutues.

manquantes
outliers
biaisées
obsolètes
problèmes de confidentialité (RGPD, anonymisation)

mais aussi

données redondantes
erreurs de saisie
formats incompatibles
granularité inégale / imbalance
variables mal labelisées
encodage incorrect (UTF-8, ISO, etc.)
valeurs par défaut erronées
données agrégées vs brutes non distinguées
métadonnées absentes ou incomplètes
dépendances temporelles ignorées
échelles de mesure inconsistantes
données synthétiques mal intégrées

Supervisé, non supervisé, semi-supervisé

Différences d'objectifs et de données disponibles

Supervisé : labels connus
- 2 sets de data: training et test
- exemple titanic sur Kaggle
Non supervisé : structure à découvrir (clustering)
- exemple segmentation utilisateurs, topic modeling
- dimensionality reduction
- Knn, nearest neighbour etc
Semi-supervisé : peu de labels, beaucoup de données
- reinforcement learning

Types de tâches ML supervisées

Régression
- target est continue: prix, temperature etc
Classification binaire : 0/1, vrai faux, click pas click
Classification multiclasse : plusieurs classes
- non ordonnées : rouge vert blanc
- ordonnées : grand moyen petit
- technique : on revient a la classification binaire
  - one vs one
  - one vs rest

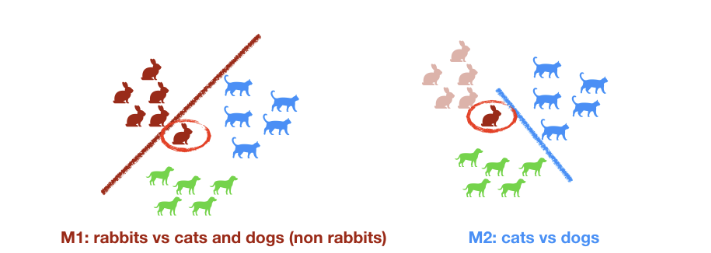
Classification multilabel : plusieurs labels

Sqrt(2)

Approximations successives

Erreur et fonction de coût

Méthode de Héron

inventée au 1er siècle apres JC par les babyloniens.

valeur d'initialisation pour x: x = 1
precision attendue: precision = 0.001

Tant que |x^2 - 2| > precision :

mettre à jour x x = (x + 2/x)/2

La suite est disponible en notebook jupyter: heron_sqrt_2.ipynb et sur Colab

En python, cela s'ecrit

x = 1
precision = 0.001
while (abs(x**2 - 2) > precision) :
    x = (x + 2/x)/2

print(x)

Converge extremenent rapide !

Erreur d'estimation

L'erreur d'estimation |x^2 - 2| est la différence en valeur absolu entre la valeur candidate au carré et 2.

x = 1
error = 1
precision = 0.001
n_iter = 0

while error > precision:
    # Update the estimation
    x = (x + 2/x) / 2
    # Update the error with the new value of x
    n_iter += 1
    print(f"Iteration {n_iter}: x = {x}")
    error = abs(x**2 - 2)

print(f"Approximation of √2: {x}")
print(f"Final error: {error}")
print(f"Difference: {abs(x - 2**0.5)}")
print(f"Number of iterations: {n_iter}")

Learning rate

on peut modifier la vitesse de convergence avec un coefficient moderateur de la mise a jour

On peut réecrire x = (x + 2/x) / 2 => x = x + lambda * (2/x - x) avec lambda = 1/2 ou une autre valeur

lambda petit => convergence lente lambda grand => convergence rapide mais peut exploser

x = 1
error = 1
precision = 0.001
lambda_val = 0.1
n_iter = 0
while error > precision:
    # Update the estimation
    x = x + lambda_val * (2/x - x)
    n_iter += 1
    print(f"Iteration {n_iter}: x = {x}")
    # Update the error with the new value of x
    error = abs(x**2 - 2)

print(f"Approximation of √2: {x}")
print(f"Final error: {error}")
print(f"Difference: {abs(x - 2**0.5)}")

fct de cout

au lieu de minimiser l'erreur absolue, on peut minimiser l'erreur quadratique

error = (x^2 - 2)^2


x = 1
error = 1
precision = 0.001
lambda_val = 0.1
n_iter = 0

def cost_function(x):
    # return abs(x**2 - 2)
    return (x**2 -2)**2

while error > precision:
    # Update the estimation
    x = x + lambda_val * (2/x - x)
    n_iter += 1
    print(f"Iteration {n_iter}: x = {x}")
    # Update the error with the new value of x
    error = cost_function(x)

print(f"Approximation of √2: {x}")
print(f"Final error: {error}")
print(f"Difference: {abs(x - 2**0.5)}")

La convergence est plus rapide avec l'erreur quadratique que l'erreur absolue

resumé

fonction de cout : mesure de la difference entre la valeur predite et la valeur reelle
- Liste des fonctions de cout sur scikit-learn
learning rate : coefficient modérateur de la mise à jour
- plus petit => convergence lente
- plus grand => convergence rapide mais peut exploser

Régression linéaire

Modèle simple et interprétable
Base pour comprendre l'optimisation

Regression lineaire

Capte la tendance générale des observations.

dimension = 1: Predire une variable y à partir d'une variable x, trouver les coefficients a et b dans l'équation de la droite

y = a x + b.

dimension 2, x_1 et x_2 de y, le modèle correspond à l'équation du plan défini par

y = a x_1 + b x_2 + c

dimension N, et N variables {x_1, ..., x_N} => trouver les N coefficients c_1, ... c_N de l'équation:

y = c_1 x_1 +_ c_2 x_2 + ... + c_N x_N + c_{N+1}

Pourquoi la regression lineaire a de beaux jours devant elle

interprétabilité: le poid respectif des coefficients montre le poids relatif des variables dans la prédiction
facilité d'implémentation: en tout langage, dans toutes les librairies
rapidité de calcul: optimisée depuis des lustres les calculs sont hyper rapides
consomme peu de mémoire: étant hyper optimisé depuis longtemps

Regression polynomiale

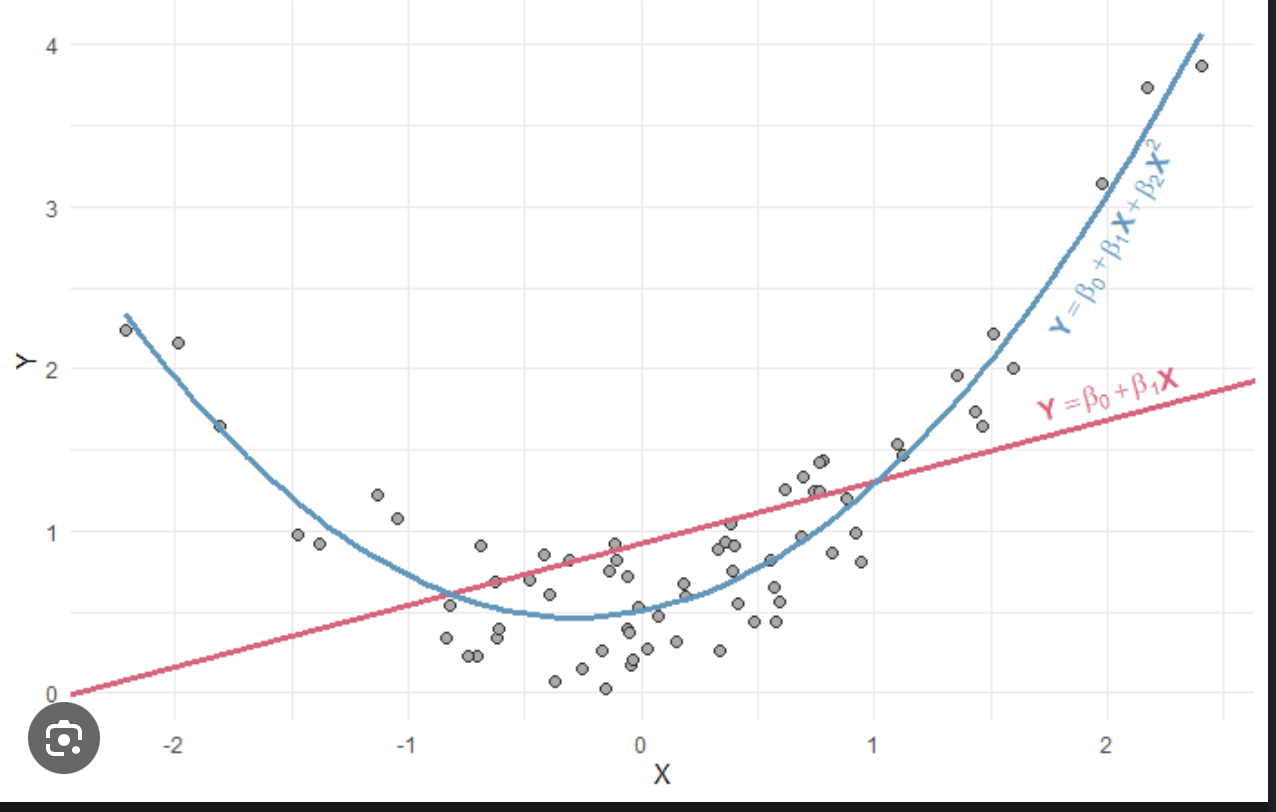
Précautions

non linéarité: la relation entre la variable cible et les prédicteurs doit être linéaire (a peu pres)
normalisation des variables: vérifier l'amplitude des valeurs des variables

le dataset advertising :

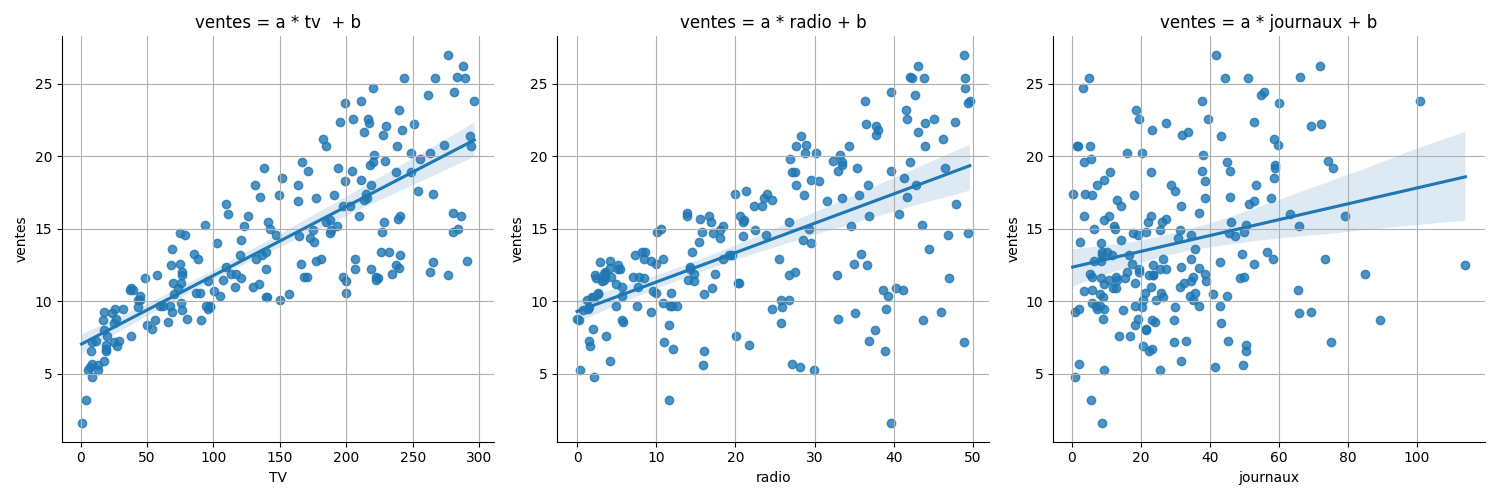
Pour aller plus loin sur la regression lineaire, voir le cours Entrenez une régression linéaire

Régression logistique

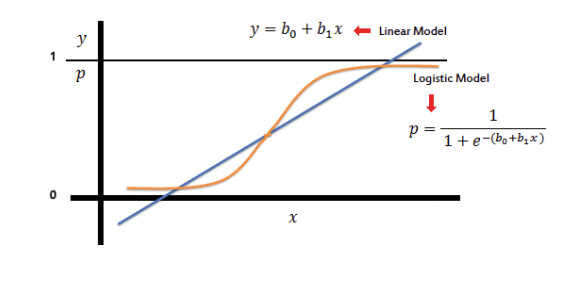
En sortie de la regression lineaire, on obtient une valeur continue non bornée
On borne cette valeur entre 0 et 1 à l'aide d'une fonction sigmoïde
on interprète cette valeur comme une probabilité d'appartenir a une classe ou a une autre
- si la probabilité est supérieure à 0.5, on predit la classe 1
- si la probabilité est inférieure à 0.5, on predit la classe 0

Gradient descent

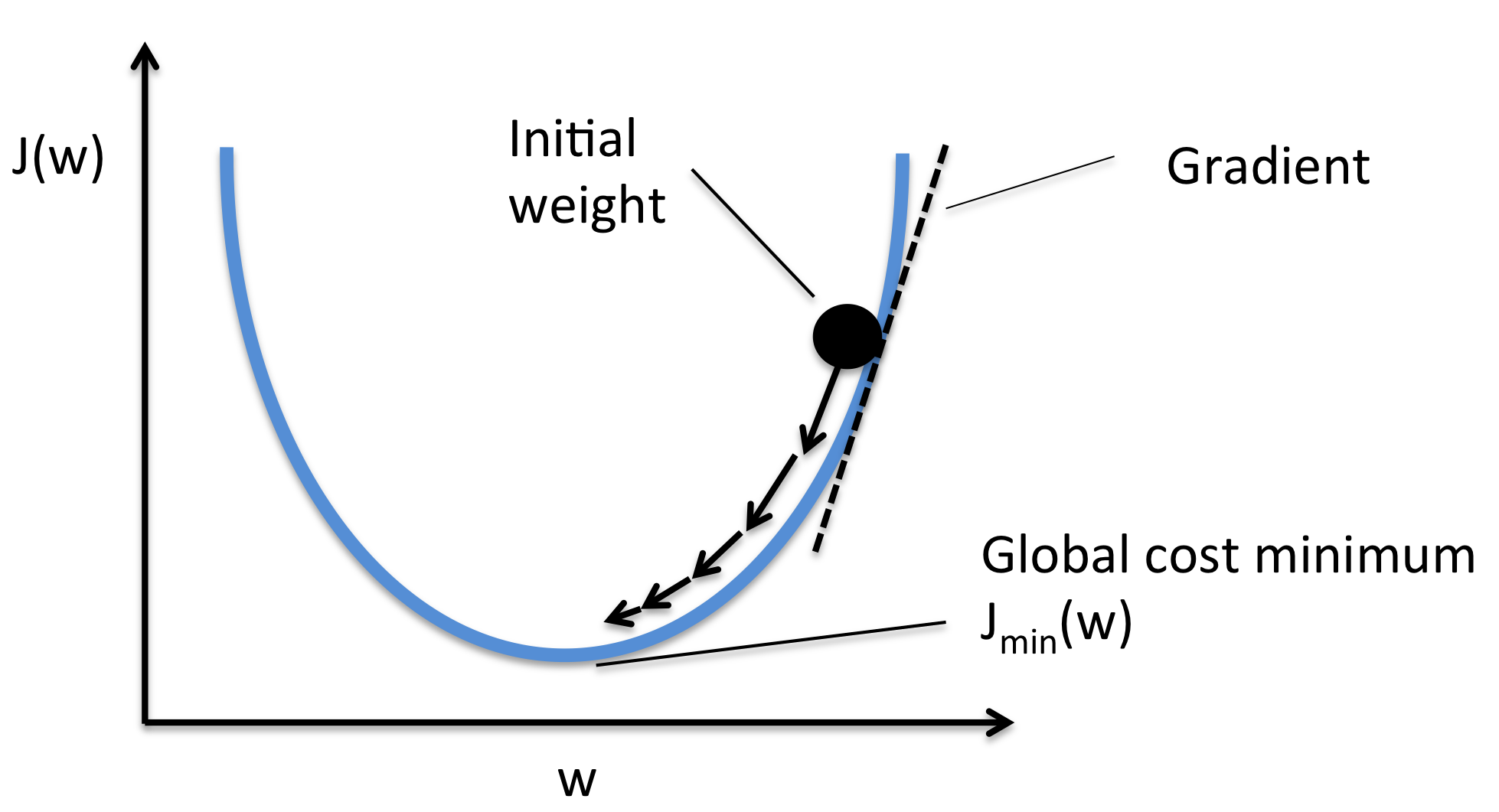
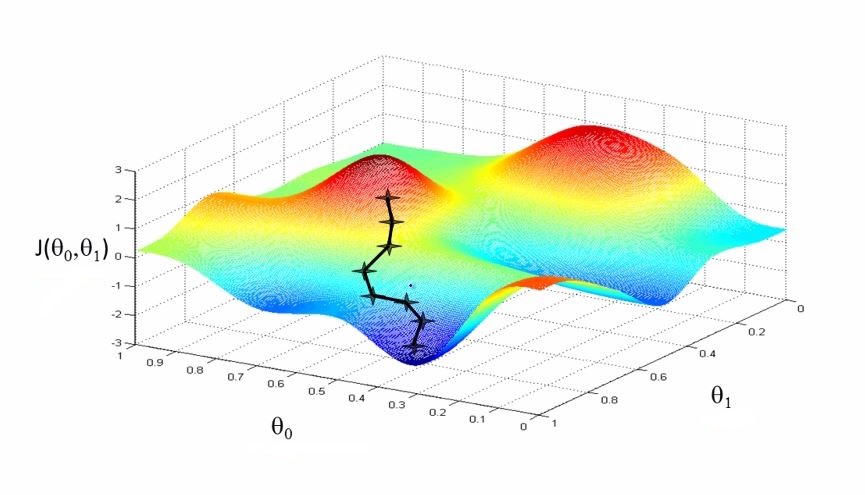
Descente de gradient

Objectif : Trouver le minimum d'une fonction dérivable $f(x)$ (la fonction de cout)

Principe : Itération selon la direction opposée au gradient

$x_{n+1} = x_n - \eta \nabla f(x_n)$

où $\eta$ est le taux d'apprentissage (learning rate) et $\nabla f(x_n)$ le gradient, la derivée de la fonction $f(x)$ (= le gradient)

Qu'est-ce que le gradient ?

Le gradient, c'est la pente de la fonction à un point donné.

Il indique dans quelle direction monter pour augmenter la fonction
Plus le gradient est grand, plus la pente est raide

Démonstration : Fonction Polynomiale

Exemple : Minimiser $f(x) = x^2 - 4x + 5$

Dérivée : $f'(x) = 2x - 4$

Algorithme :

Initialisation : $x_0 = 0$
Itération : $x_{n+1} = x_n - \eta \cdot (2x_n - 4)$
Avec $\eta = 0.1$ : convergence vers $x^* = 2$ (minimum)

Résultat : $f(2) = 1$ est le minimum global

voir le colab

voir slides gradient stochastique

Overfitting

Trop bien sur les données d'entraînement
Généralise mal

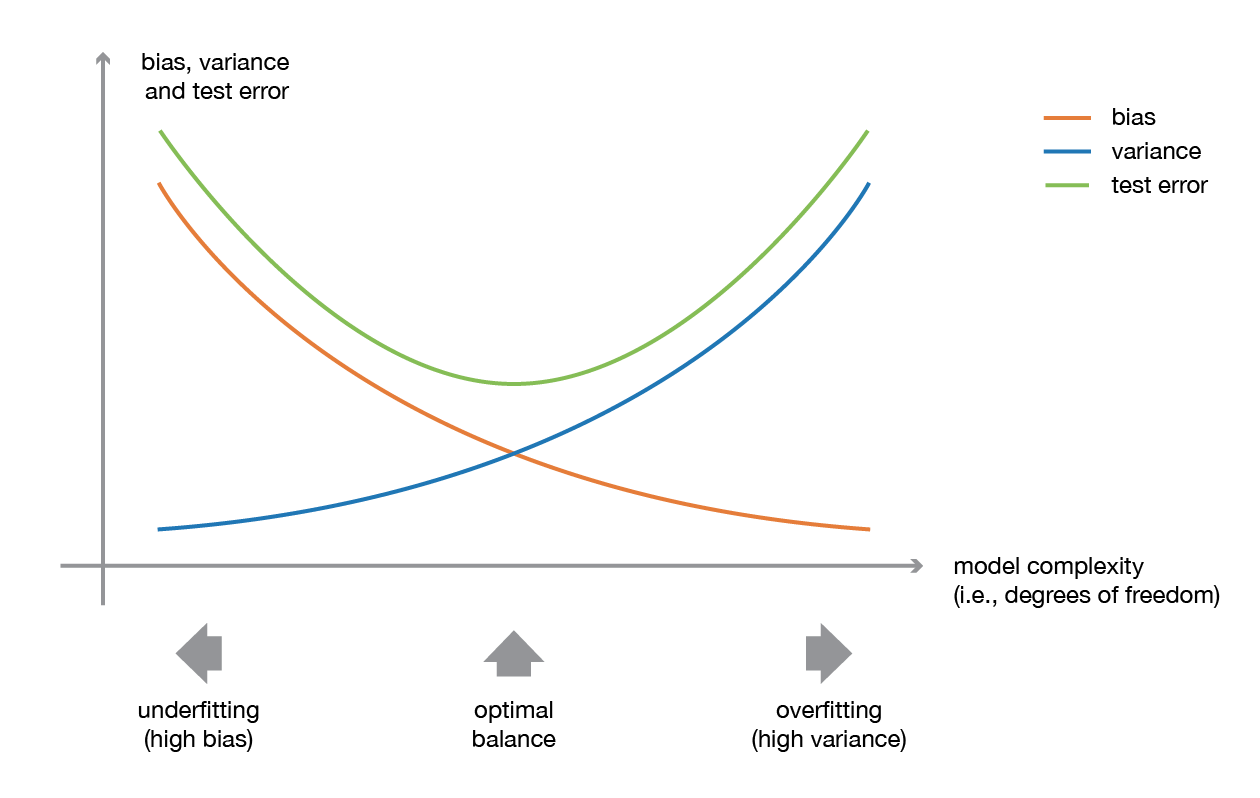
Biais-variance

Biais élevé : modèle trop simple
Variance élevée : modèle trop sensible

No free lunch

Aucun modèle ne gagne partout
Le contexte dicte le choix

aucun algorithme n’est universellement supérieur à un autre sur l’ensemble des problèmes possibles.

Il n’existe pas d’algorithme qui performe systématiquement mieux que tous les autres, quelle que soit la tâche ou la distribution des données. Toute méthode optimisée pour un type de problème (ex : classification d’images) peut être surpassée par une autre sur un problème différent (ex : prédiction de séries temporelles).

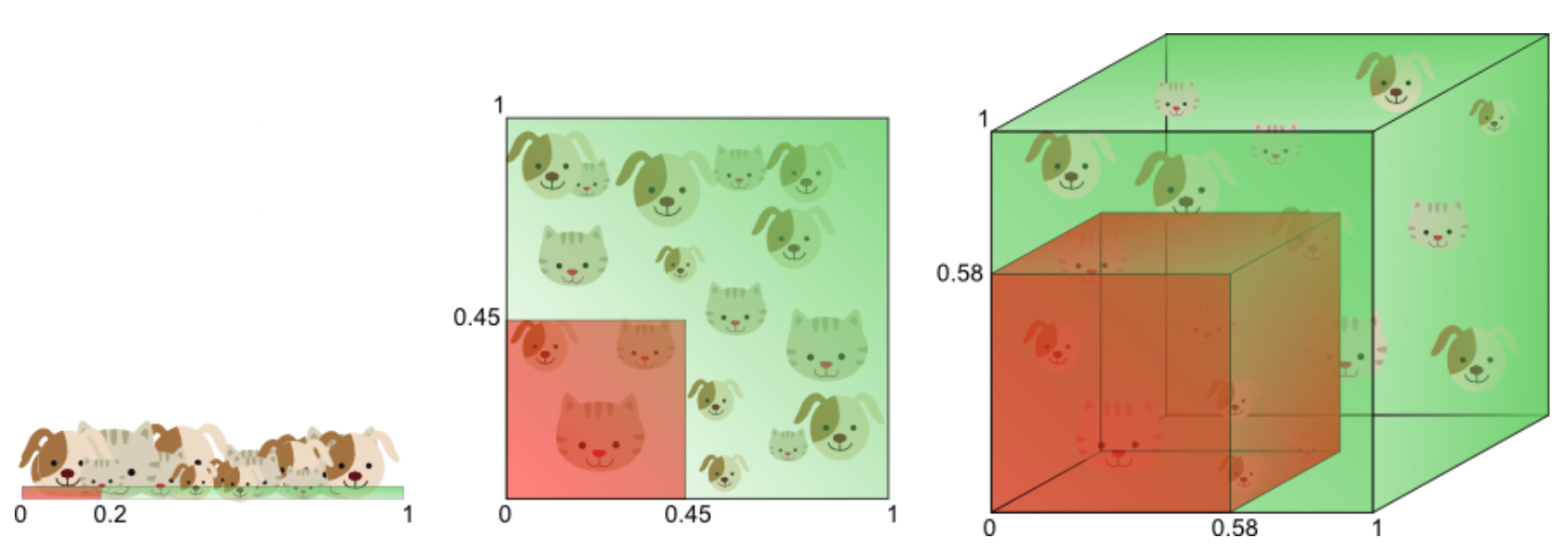
Malédiction de la dimension

curse of dimension

Les données deviennent rares en haute dimension
Les distances perdent leur sens

Algorithmes gloutons

Choix locaux rapides
Pas toujours optimal globalement

principe de choisir, à chaque itération, l’option qui semble la meilleure à court terme, sans revenir en arrière. Cette approche est simple, efficace pour certains problèmes, mais ne garantit pas toujours l’optimalité globale. Caractéristiques clés :

Déterministes : pas de hasard, choix basés sur une heuristique claire.
Locaux : décision prise uniquement en fonction des données disponibles à l’étape courante.
Irréversibles : une fois un choix fait, il n’est pas révisé.
Rapides : souvent une complexité polynomiale (ex : O(n log n) pour Dijkstra).

C’est souvent plus rapide et moins gourmand en ressources que des méthodes exhaustives (ex : recherche combinatoire). Idéal pour des problèmes où une solution "suffisamment bonne" suffit.

L’algorithme est sensible à l’ordre des données ou des décisions. Un mauvais choix précoce peut dégrader la performance finale.

Intermission

Metropolis - Fritz Lang - 1927

41'37"

TD Gradient stochastique

Notebook dispo sur

1 / 0