Des Séquences aux Transformers
Attention, Self-Attention
l'architecture qui a tout changé
Plan du cours
Trois grandes parties.
- Les modèles séquence-à-séquence (seq2seq) fondés sur les RNN, en comprenant pourquoi ils atteignent leurs limites sur les longues séquences.
- Le mécanisme d'attention de Bahdanau, qui permet au décodeur de "regarder en arrière" vers l'encodeur.
- L'architecture Transformer, qui abandonne complètement la récurrence au profit de l'attention. Base de tous les grands modèles de langage actuels (GPT, BERT, LLaMA, etc.).
Crédits : les posts de Jay Alammar,
Partie 1
Seq2Seq et le goulot d'étranglement / bottleneck
Embedding
La couche Embedding de Keras transforme des indices entiers (identifiants de mots) en vecteurs denses de taille fixe.
Concrètement, c'est une table de lookup : une matrice de poids de taille (vocab_size, embedding_dim) où chaque ligne correspond à un mot du vocabulaire.
from keras import layers
# Vocabulaire de 10 000 mots → vecteurs de 256 dimensions
embedding = layers.Embedding(input_dim=10000, output_dim=256)
# Entrée : indices de mots, ex. [42, 7, 153]
# Sortie : les 3 vecteurs correspondants, shape (3, 256)
input_dim: taille du vocabulaire (nombre de mots possibles)output_dim: dimension du vecteur dense pour chaque mot
Les poids de cette matrice sont appris pendant l'entraînement : le réseau découvre lui-même quelles représentations vectorielles sont utiles pour la tâche.
- À l'initialisation : les vecteurs sont aléatoires, aucun sens sémantique.
- Après entraînement : les vecteurs capturent une sémantique liée à la tâche. Les mots proches en sens (roi/reine, chat/chien) finissent avec des vecteurs proches — c'est le même principe que Word2Vec, sauf que l'embedding est appris conjointement avec le reste du réseau.
Embedding Keras vs modèle Hugging Face
layers.Embedding (Keras) | Modèle HF (ex. sentence-transformers) | |
|---|---|---|
| Initialisation | Poids aléatoires | Poids pré-entraînés sur des milliards de textes |
| Représentation | Statique : un mot = un vecteur, quel que soit le contexte | Contextuelle : le même mot a un vecteur différent selon la phrase |
| Lookup | Simple accès à une ligne de matrice | Passe complète dans un Transformer (self-attention sur toute la phrase) |
| Sémantique | Apprise sur votre tâche (commence à zéro) | Déjà riche d'une sémantique générale (milliards de textes) |
| Entraînement | Doit être entraîné sur votre tâche | Utilisable tel quel (transfer learning) |
# Keras : "avocat" a toujours le même vecteur
embedding = layers.Embedding(10000, 256)
# embedding(42) → toujours le même vecteur, que ce soit
# "l'avocat a plaidé non coupable" ou "une salade d'avocat"
# Hugging Face : "avocat" a un vecteur différent selon le contexte
from sentence_transformers import SentenceTransformer
model = SentenceTransformer("all-MiniLM-L6-v2")
model.encode("l'avocat a plaidé non coupable") # vecteur A
model.encode("une salade d'avocat") # vecteur B (≠ A)
Dans un Transformer, la couche Embedding de Keras ne sert qu'au premier étage : elle fournit les vecteurs initiaux. C'est ensuite la self-attention qui rend ces représentations contextuelles — exactement ce que font les modèles Hugging Face en interne.
Rappel : le RNN pas à pas
À chaque pas de temps t, un RNN calcule :
ht=f(Wh⋅ht−1+Wx⋅xt+b)
où xt est l'embedding du mot courant et ht−1 l'état caché précédent.
- La fonction f est typiquement une tangente hyperbolique ou, dans le cas du LSTM, un mécanisme de portes (forget, input, output) qui contrôle le flux d'information.
Le problème fondamental : toute l'information de la phrase d'entrée doit passer par un unique vecteur hT de taille fixe (256, 512, ou 1024 dimensions).
Le RNN en Keras
import keras
from keras import layers
# Encodeur LSTM simple
encoder_input = layers.Input(shape=(None, embedding_dim))
encoder_lstm = layers.LSTM(256, return_state=True)
_, state_h, state_c = encoder_lstm(encoder_input)
# state_h = le fameux vecteur de contexte
encoder_states = [state_h, state_c]
encoder_input est un placeholder : il déclare la forme des données d'entrée sans faire de calcul. shape=(None, embedding_dim) signifie "une séquence de longueur variable, où chaque mot est déjà un vecteur de dimension embedding_dim". Ici l'embedding est supposé fait en amont — dans le modèle complet plus loin, on utilisera une couche Embedding intégrée.
Ce state_h de 256 dimensions doit résumer une phrase entière qu'elle fasse 5 ou 50 mots.
Le modèle Seq2Seq
Un modèle seq2seq
- input: une séquence d'entrée
- output: une séquence de sortie
une phrase en français -> la phrase traduite en anglais
L'architecture repose sur deux composants :
- un encodeur qui lit l'entrée mot par mot et compresse l'information dans un vecteur,
- un décodeur qui génère la sortie à partir de ce vecteur.
Pourquoi encodeur + decodeur
L'idée est simple : comprendre et parler sont deux tâches différentes.
Quand tu traduis du français vers l'anglais, tu fais deux choses distinctes :
- Tu lis et tu comprends la phrase française → c'est l'encodeur. Il transforme une séquence de mots en une représentation interne du sens de la phrase.
- Tu formules et tu écris la phrase anglaise → c'est le décodeur. Il prend cette représentation du sens et génère les mots un par un dans la langue cible.
Pourquoi ne pas utiliser un seul réseau ?:
Parce que les deux langues n'ont pas la même structure. "J'aime la musique" c'est 4 mots, "I love music" c'est 3 mots. L'ordre peut changer, la grammaire est différente. On ne peut pas faire du mot-à-mot.
La séparation encodeur/décodeur permet de découpler la compréhension de la génération.
Entre les deux, il y a une représentation abstraite du sens, indépendante de la langue. C'est comme un interprète qui écoute d'abord tout le message, le comprend dans sa tête, puis le reformule dans l'autre langue.
Seq2Seq en Keras
from keras import layers, Model
import numpy as np
# === HYPERPARAMÈTRES ===
vocab_size_src = 10000 # Taille du vocabulaire source (ex: français) → 10 000 mots possibles
vocab_size_tgt = 8000 # Taille du vocabulaire cible (ex: anglais) → 8 000 mots possibles
embedding_dim = 256 # Chaque mot sera représenté par un vecteur de 256 nombres
hidden_dim = 512 # Taille de la "mémoire interne" du LSTM (le fameux post-it)
# =============================================
# ENCODEUR — Lit la phrase source et la résume
# =============================================
# Entrée : une séquence d'entiers (chaque entier = un mot du vocabulaire source)
# shape=(None,) → la longueur de la phrase peut varier
enc_input = layers.Input(shape=(None,), name="encoder_input")
# Embedding : transforme chaque mot (un simple numéro) en un vecteur riche de 256 dimensions
# Ex: le mot n°42 devient [0.12, -0.8, 0.3, ...] (256 valeurs)
enc_emb = layers.Embedding(vocab_size_src, embedding_dim)(enc_input)
# LSTM de l'encodeur : lit la séquence mot par mot
# return_state=True → on récupère l'état final de la mémoire :
# - enc_h = "hidden state" (résumé de ce que le LSTM a compris)
# - enc_c = "cell state" (mémoire à long terme du LSTM)
# On jette la sortie séquentielle (_) car on veut juste le résumé final
_, enc_h, enc_c = layers.LSTM(hidden_dim, return_state=True)(enc_emb)
# >>> À ce stade : toute la phrase source est compressée dans enc_h et enc_c
# >>> Ce sont deux vecteurs de 512 nombres chacun
# =============================================
# DÉCODEUR — Génère la traduction mot par mot
# =============================================
# Entrée : la phrase cible décalée d'un cran (technique du "teacher forcing")
# Pendant l'entraînement, on lui donne la bonne traduction en entrée
# Ex: si la cible est "I love music", l'entrée décodeur est "<START> I love music"
dec_input = layers.Input(shape=(None,), name="decoder_input")
# Même principe : chaque mot cible devient un vecteur de 256 dimensions
dec_emb = layers.Embedding(vocab_size_tgt, embedding_dim)(dec_input)
# LSTM du décodeur :
# - return_sequences=True → on veut une sortie pour CHAQUE mot (pas juste le dernier)
# - return_state=True → on récupère aussi les états (utile pour l'inférence)
dec_lstm = layers.LSTM(hidden_dim, return_sequences=True, return_state=True)
# ⭐ LA LIGNE CLÉ : initial_state=[enc_h, enc_c]
# On initialise le décodeur avec le "post-it" de l'encodeur
# C'est LE SEUL LIEN entre l'encodeur et le décodeur
# Toute la compréhension de la phrase source passe par ces 2 vecteurs
dec_output, _, _ = dec_lstm(dec_emb, initial_state=[enc_h, enc_c])
# =============================================
# COUCHE DE SORTIE — Choisir le mot suivant
# =============================================
# Pour chaque position, on calcule une probabilité sur les 8000 mots du vocabulaire cible
# softmax → les 8000 valeurs s'additionnent à 1 (ce sont des probabilités)
# Le mot avec la plus haute probabilité est le mot prédit
output = layers.Dense(vocab_size_tgt, activation="softmax")(dec_output)
# =============================================
# ASSEMBLAGE DU MODÈLE
# =============================================
# Le modèle prend 2 entrées (phrase source + phrase cible décalée)
# et produit 1 sortie (les probabilités de chaque mot cible)
model = Model([enc_input, dec_input], output)
# sparse_categorical_crossentropy car nos cibles sont des entiers (pas du one-hot)
model.compile(optimizer="adam", loss="sparse_categorical_crossentropy")
Le point essentiel à retenir : initial_state=[enc_h, enc_c] — ces deux vecteurs de 512 dimensions sont le seul canal de communication entre l'encodeur et le décodeur. Que la phrase source fasse 5 mots ou 500, tout doit tenir dans ce post-it de taille fixe. C'est exactement la limitation que l'attention viendra résoudre.
Vecteur de contexte
L'encodeur est un RNN (souvent un LSTM ou GRU).
À chaque pas de temps, il reçoit le word embedding du mot courant et son état caché précédent, et produit un nouvel état caché.
Le dernier état caché constitue le vecteur de contexte : la seule information transmise au décodeur.
Le goulot d'étranglement du contexte fixe
Imaginez qu'on vous demande de traduire un paragraphe entier, mais que vous n'avez le droit de resumer que sur un post-it entre la lecture et l'écriture que le texte fasse 3 ou 300 mots
Le vecteur de contexte fixe du RNN encoder-decoder, c'est ce post-it : sa dimension ne change pas, quelle que soit la longueur de l'entrée. D'où la perte d'information sur les textes longs.
Pour des phrases courtes, ça fonctionne. Pour des phrases longues, l'information se dégrade.
C'est exactement ce qui se passe avec le vecteur de contexte. Les expériences montrent une chute significative de la qualité de traduction au-delà de 20-30 mots.
Les premiers mots de la phrase sont progressivement "oubliés" au profit des derniers : c'est le problème classique du vanishing gradient appliqué aux séquences longues, même avec des LSTM.
Partie 2
Le mécanisme d'Attention
L'idée clé de l'attention
En 2014, Bahdanau et al. proposent une solution élégante au goulot d'étranglement : plutôt que de forcer toute l'information à passer par un seul vecteur, le décodeur peut regarder tous les états cachés de l'encodeur à chaque étape de génération.
L'analogie est simple. Au lieu de prendre une seule note résumant tout le texte, vous gardez le texte source sous les yeux et vous pouvez y jeter un coup d'œil à chaque mot que vous traduisez. Naturellement, votre regard se porte sur les parties pertinentes du texte — c'est exactement ce que fait l'attention.
Schéma montrant l'encodeur qui transmet tous ses états cachés (h₁, h₂, ..., hₙ) au décodeur, au lieu d'un seul vecteur de contexte.
Attention : le calcul étape par étape
À chaque pas de décodage t, on calcule un vecteur de contexte ct spécifique :
1. Score — On mesure la pertinence de chaque état caché de l'encodeur hienc par rapport à l'état courant du décodeur st :
et,i=score(st,hienc)
2. Normalisation — On transforme les scores en poids via softmax :
αt,i=∑jexp(et,j)exp(et,i)
3. Contexte — On calcule la somme pondérée :
ct=∑iαt,i⋅hienc
Les αt,i forment une distribution de probabilité sur les mots source. En traduction français→anglais, quand le décodeur génère "student", les poids d'attention seront élevés sur "étudiant" et faibles sur les autres mots.
Le score peut être calculé de différentes façons :
| Variante | Formule |
|---|---|
| Dot product | st⊤hi |
| Général (Luong) | st⊤Wahi |
| Additif (Bahdanau) | va⊤tanh(W1st+W2hi) |
Visualiser l'alignement
Quand on affiche la matrice d'attention α pour une paire de phrases, on obtient une matrice d'alignement qui montre quels mots source contribuent à chaque mot cible.
Un résultat remarquable : le modèle apprend seul l'alignement entre les langues. Par exemple, pour "la zone économique européenne" → "the European Economic Area", l'attention apprend automatiquement l'inversion de l'ordre des adjectifs entre le français et l'anglais.
Matrice d'alignement (heatmap) pour la traduction d'une phrase français→anglais, montrant comment les mots se correspondent. On voit clairement l'inversion de l'ordre pour "zone économique européenne" → "European Economic Area".

Attention avec Keras
from keras import layers, Model
hidden_dim = 512
# --- ENCODEUR avec return_sequences ---
enc_input = layers.Input(shape=(None,), name="encoder_input")
enc_emb = layers.Embedding(vocab_size_src, embedding_dim)(enc_input)
enc_outputs, enc_h, enc_c = layers.LSTM(
hidden_dim, return_sequences=True, return_state=True # return_sequences=True !
)(enc_emb)
# --- DÉCODEUR ---
dec_input = layers.Input(shape=(None,), name="decoder_input")
dec_emb = layers.Embedding(vocab_size_tgt, embedding_dim)(dec_input)
dec_outputs, _, _ = layers.LSTM(
hidden_dim, return_sequences=True, return_state=True
)(dec_emb, initial_state=[enc_h, enc_c])
# --- ATTENTION (Luong dot-product) ---
# scores : (batch, dec_len, enc_len)
attention_scores = layers.Dot(axes=[2, 2])([dec_outputs, enc_outputs])
attention_weights = layers.Activation("softmax")(attention_scores)
# contexte : (batch, dec_len, hidden_dim)
context = layers.Dot(axes=[2, 1])([attention_weights, enc_outputs])
# concaténation et projection
concat = layers.Concatenate()([dec_outputs, context])
output = layers.Dense(hidden_dim, activation="tanh")(concat)
output = layers.Dense(vocab_size_tgt, activation="softmax")(output)
model = Model([enc_input, dec_input], output)
La différence clé avec le modèle précédent : return_sequences=True sur l'encodeur. On garde maintenant tous les états cachés, pas seulement le dernier.
Ce que l'attention a changé — et ses limites
L'attention a résolu le goulot d'étranglement et amélioré considérablement la traduction automatique, surtout sur les phrases longues.
Mais le modèle reste fondamentalement séquentiel : l'encodeur RNN doit traiter les mots un par un, dans l'ordre. Impossible de paralléliser le calcul. Sur un GPU moderne avec des milliers de nodes, c'est un gâchis monumental.
De plus, même avec des LSTM et l'attention, l'information sur les dépendances à très longue distance reste fragile. Le RNN doit propager les gradients à travers de nombreux pas de temps.
En 2017, l'équipe de Google Brain pose une question audacieuse dans un article au titre provocateur : et si on se débarrassait complètement de la récurrence ?
Partie 3
Le Transformer
"Attention Is All You Need"
Vaswani et al., 2017
Vue d'ensemble du Transformer
Le Transformer conserve l'architecture encodeur-décodeur, mais remplace entièrement les RNN par des couches d'attention. L'article original empile 6 encodeurs et 6 décodeurs.
Chaque bloc encodeur contient deux sous-couches:
- une couche de self-attention multi-têtes
- un réseau feed-forward position par position
Chaque bloc décodeur contient trois sous-couches:
- une couche de self-attention masquée
- une couche d'attention croisée (encoder-decoder)
- un réseau feed-forward
Chaque sous-couche est entourée d'une connexion résiduelle et d'une normalisation de couche.
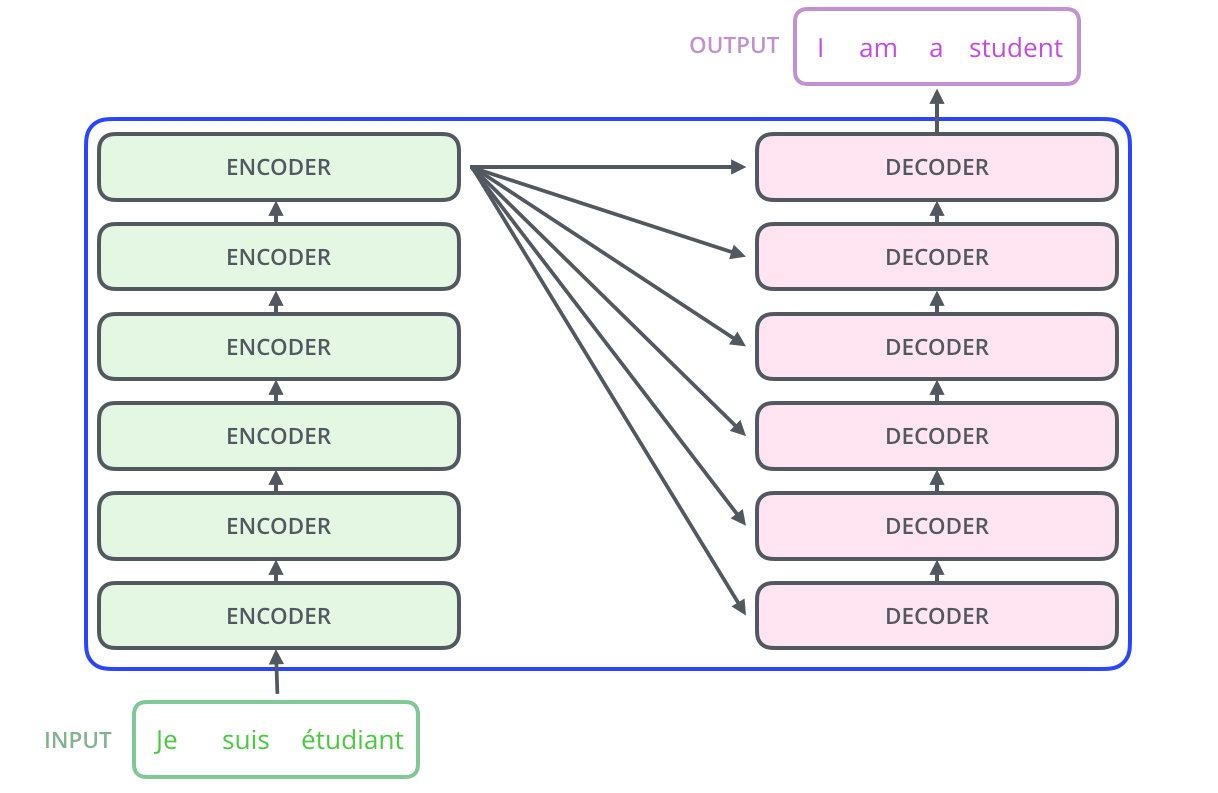
Architecture complète du Transformer. À gauche, la pile de 6 encodeurs. À droite, la pile de 6 décodeurs. Montrer les connexions entre le dernier encodeur et chaque décodeur (K, V envoyés à l'attention croisée). (Alammar: The_transformer_encoders_decoders.png + The_transformer_encoder_decoder_stack.png)
Pourquoi abandonner les RNN ?
Le Transformer traite tous les mots en parallèle. Là où un LSTM avec une phrase de 50 mots nécessite 50 étapes séquentielles, le Transformer n'en fait qu'une seule passe matricielle. En pratique, le temps d'entraînement est divisé par un facteur significatif.
Mais comment le modèle peut-il capturer les relations entre les mots s'il les traite tous en même temps ? C'est ici qu'intervient la self-attention : chaque mot peut "regarder" tous les autres mots de la séquence en une seule opération. Le mot "it" dans "The animal didn't cross the street because it was too tired" peut directement s'associer au mot "animal", sans avoir à propager l'information à travers une chaîne de states cachés.

Visualisation de la self-attention sur la phrase "The animal didn't cross the street because it was too tired". Des lignes colorées relient "it" aux mots auxquels il prête attention, avec "animal" fortement pondéré.
Self-Attention : l'intuition Query-Key-Value
L'idée centrale est une analogie avec un système de recherche d'information. Pour chaque mot de la séquence, on crée trois vecteurs :
Query (Q) — "Que cherche ce mot ?" C'est la question que pose le mot courant.
Key (K) — "Qu'est-ce que ce mot offre comme information ?" C'est l'étiquette que porte chaque mot.
Value (V) — "Quelle information ce mot transporte réellement ?" C'est le contenu.
Le score d'attention entre deux mots est le produit scalaire entre la Query de l'un et la Key de l'autre. Ce score mesure la compatibilité : à quel point ce que je cherche correspond à ce que l'autre offre. Les scores sont ensuite normalisés par softmax pour obtenir des poids, et la sortie est une somme pondérée des Values.
C'est comme un moteur de recherche interne à la phrase : chaque mot lance une requête et récupère les informations pertinentes des autres mots.
Self-Attention : le calcul vectoriel
Pour un mot xi avec son embedding (ou sa représentation venant de la couche précédente), on projette vers Q, K, V via des matrices de poids apprises :
qi=xi⋅WQ,ki=xi⋅WK,vi=xi⋅WV
L'embedding a une dimension dmodel=512.
Les vecteurs Q, K, V ont une dimension dk=64
Le score entre le mot i (query) et le mot j (key) :
scoreij=qi⋅kj⊤
On divise par dk pour stabiliser les gradients :
scoreijscaled=dkqi⋅kj⊤
Pourquoi dk ? Quand dk est grand, les produits scalaires deviennent grands en magnitude, ce qui pousse le softmax dans ses zones saturées (gradients quasi-nuls). Diviser par dk ramène la variance des scores à 1.
Après softmax et pondération des values :
zi=∑jsoftmax(scoreijscaled)⋅vj
Self-Attention : la formule matricielle
En pratique, on ne calcule pas mot par mot. On empile tous les embeddings dans une matrice X de taille (n×dmodel) et on calcule tout en une seule opération :
Q=X⋅WQ,K=X⋅WK,V=X⋅WV
Attention(Q,K,V)=softmax(dkQ⋅K⊤)⋅V
La matrice Q⋅K⊤ a une taille (n×n) — chaque élément (i,j) mesure à quel point le mot i doit prêter attention au mot j. Après softmax (ligne par ligne), on multiplie par V pour obtenir les nouvelles représentations.
Implémentation NumPy de la self-attention
import numpy as np
def self_attention(X, W_q, W_k, W_v):
"""
X : (seq_len, d_model) — embeddings de la séquence
W_q/k/v : (d_model, d_k) — matrices de projection
"""
Q = X @ W_q # (seq_len, d_k)
K = X @ W_k
V = X @ W_v
d_k = Q.shape[-1]
# Scores : (seq_len, seq_len)
scores = Q @ K.T / np.sqrt(d_k)
# Softmax ligne par ligne
exp_scores = np.exp(scores - scores.max(axis=-1, keepdims=True))
weights = exp_scores / exp_scores.sum(axis=-1, keepdims=True)
# Sortie : somme pondérée des values
output = weights @ V # (seq_len, d_k)
return output, weights
# Exemple avec 4 mots, d_model=8, d_k=4
np.random.seed(42)
X = np.random.randn(4, 8)
W_q = np.random.randn(8, 4) * 0.1
W_k = np.random.randn(8, 4) * 0.1
W_v = np.random.randn(8, 4) * 0.1
out, attn = self_attention(X, W_q, W_k, W_v)
print("Poids d'attention:\n", np.round(attn, 3))
Observez que weights est une matrice (n×n) dont chaque ligne somme à 1. C'est la "carte d'attention" qui montre qui regarde qui.
Multi-Head Attention : pourquoi plusieurs têtes ?
Une seule tête d'attention ne capture qu'un seul "type" de relation. Mais dans une phrase, les relations sont multiples : syntaxiques, sémantiques, coréférentielles. Le Transformer utilise 8 têtes d'attention en parallèle, chacune avec ses propres matrices WiQ,WiK,WiV.
Chaque tête opère dans un sous-espace de dimension dk=dmodel/h=512/8=64. Les 8 sorties sont concaténées puis projetées :
MultiHead(Q,K,V)=Concat(head1,...,head8)⋅WO
où chaque headi=Attention(QWiQ,KWiK,VWiV)
La matrice WO a une taille (8×64,512)=(512,512), ramenant la sortie à la dimension dmodel.
Le coût total est comparable à une seule tête de dimension 512, puisque 8×64=512. On ne paye pas plus cher, mais on obtient 8 "points de vue" différents sur la séquence.
Multi-Head en Keras
from keras import layers
# Keras fournit une couche MultiHeadAttention prête à l'emploi
mha = layers.MultiHeadAttention(
num_heads=8,
key_dim=64, # d_k par tête
value_dim=64, # d_v par tête (souvent = d_k)
)
# Pour de la self-attention : query = key = value = même séquence
# x shape: (batch_size, seq_len, d_model=512)
attention_output = mha(query=x, key=x, value=x) # (batch, seq_len, 512)
# Avec un masque causal (pour le décodeur) :
attention_output = mha(
query=x, key=x, value=x,
use_causal_mask=True # masque les positions futures
)
La couche MultiHeadAttention de Keras encapsule toute la logique : projections Q/K/V, split en têtes, scaled dot-product, concaténation, projection de sortie. En une ligne, vous avez le cœur du Transformer.
Encodage positionnel : donner le sens de l'ordre
Le Transformer traite tous les mots simultanément — il n'a donc aucune notion d'ordre. Les phrases "le chat mange la souris" et "la souris mange le chat" produiraient la même représentation sans mécanisme supplémentaire.
La solution : ajouter un vecteur de position à chaque embedding avant de l'envoyer dans l'encodeur. L'article original utilise des fonctions sinusoïdales :
PE(pos,2i)=sin(100002i/dmodelpos)
PE(pos,2i+1)=cos(100002i/dmodelpos)
Chaque dimension du vecteur oscille à une fréquence différente, créant un "code" unique pour chaque position.
📌 IMAGE : Heatmap des encodages positionnels. En ligne : la position (0 à 50+). En colonne : les dimensions (0 à 511). On voit les sinusoïdes de fréquences croissantes — la moitié gauche (sinus) et droite (cosinus). (Alammar: transformer_positional_encoding_large_example.png)
Un avantage clé : le modèle peut généraliser à des séquences plus longues que celles vues à l'entraînement, car les fonctions sinusoïdales sont définies pour toute position.
Encodage positionnel en code
import numpy as np
def positional_encoding(max_len, d_model):
"""Génère la matrice d'encodage positionnel (max_len, d_model)."""
pe = np.zeros((max_len, d_model))
position = np.arange(max_len)[:, np.newaxis] # (max_len, 1)
div_term = 10000 ** (np.arange(0, d_model, 2) / d_model) # (d_model/2,)
pe[:, 0::2] = np.sin(position / div_term) # dimensions paires
pe[:, 1::2] = np.cos(position / div_term) # dimensions impaires
return pe
pe = positional_encoding(100, 512)
print(pe.shape) # (100, 512)
# pe[0] = position 0, pe[1] = position 1, etc.
En Keras, on peut l'intégrer comme une couche personnalisée ou simplement l'ajouter au tensor d'embeddings :
class TransformerEmbedding(layers.Layer):
def __init__(self, vocab_size, d_model, max_len=5000):
super().__init__()
self.embedding = layers.Embedding(vocab_size, d_model)
self.pe = positional_encoding(max_len, d_model).astype("float32")
self.d_model = d_model
def call(self, x):
seq_len = x.shape[1]
# On multiplie l'embedding par √d_model (convention du papier)
return self.embedding(x) * np.sqrt(self.d_model) + self.pe[:seq_len]
Connexions résiduelles et normalisation
Chaque sous-couche du Transformer (self-attention, feed-forward) est enveloppée dans un schéma Add & Norm :
output=LayerNorm(x+SubLayer(x))
La connexion résiduelle (x+SubLayer(x)) permet aux gradients de circuler directement à travers les couches, facilitant l'entraînement de réseaux profonds. C'est la même idée que dans ResNet.
La normalisation de couche stabilise les activations en normalisant sur la dimension des features (contrairement au batch norm qui normalise sur la dimension du batch). Pour chaque vecteur, on centre et réduit, puis on applique un scale/shift appris.
📌 IMAGE : Schéma d'un bloc encodeur montrant le flux : Input → Self-Attention → Add & Norm → Feed-Forward → Add & Norm → Output. Avec des flèches de skip connection. (Alammar: transformer_resideual_layer_norm_2.png)
Le réseau Feed-Forward
Après la self-attention, chaque position passe indépendamment par le même réseau feed-forward à deux couches :
FFN(x)=ReLU(x⋅W1+b1)⋅W2+b2
La dimension intérieure est dff=2048, soit 4× la taille de dmodel=512. C'est dans cette couche que le modèle effectue la "réflexion" sur les informations agrégées par l'attention. On peut l'interpréter comme une mémoire associative position par position.
def feed_forward_block(d_model=512, d_ff=2048):
return keras.Sequential([
layers.Dense(d_ff, activation="relu"), # expansion 512 → 2048
layers.Dense(d_model), # compression 2048 → 512
])
Un point important : ce réseau est appliqué identiquement et indépendamment à chaque position. Il n'y a pas d'interaction entre positions ici — toute l'interaction inter-mots se fait dans la couche d'attention.
Un bloc encodeur complet
class TransformerEncoderBlock(layers.Layer):
def __init__(self, d_model=512, num_heads=8, d_ff=2048, dropout_rate=0.1):
super().__init__()
self.mha = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=d_model // num_heads
)
self.ffn = keras.Sequential([
layers.Dense(d_ff, activation="relu"),
layers.Dense(d_model),
])
self.norm1 = layers.LayerNormalization()
self.norm2 = layers.LayerNormalization()
self.dropout1 = layers.Dropout(dropout_rate)
self.dropout2 = layers.Dropout(dropout_rate)
def call(self, x, training=False):
# Self-attention + résidu + norm
attn_output = self.mha(query=x, key=x, value=x)
attn_output = self.dropout1(attn_output, training=training)
x = self.norm1(x + attn_output)
# Feed-forward + résidu + norm
ffn_output = self.ffn(x)
ffn_output = self.dropout2(ffn_output, training=training)
x = self.norm2(x + ffn_output)
return x
On empile 6 de ces blocs pour former l'encodeur complet. Chaque bloc raffine les représentations : les couches basses capturent les relations locales (syntaxe), les couches hautes les relations globales (sémantique).
Le décodeur
Masked Self-Attention et Attention Croisée
Le décodeur : trois sous-couches
Le décodeur est plus complexe que l'encodeur car il ajoute une couche et un mécanisme de masquage. Ses trois sous-couches sont :
1. Self-attention masquée — Le décodeur ne doit pas "tricher" en regardant les mots futurs. Quand il génère le 3e mot, il ne peut voir que les mots 1 et 2. On applique un masque triangulaire qui met −∞ aux positions futures avant le softmax, ce qui produit des poids d'attention nuls pour ces positions.
2. Attention croisée (encoder-decoder) — Les Queries viennent du décodeur, mais les Keys et Values viennent de la sortie de l'encodeur. C'est l'équivalent de l'attention de Bahdanau, mais sans récurrence. Le décodeur "interroge" les représentations de la phrase source.
3. Feed-Forward — Identique à celui de l'encodeur.
📌 IMAGE : Architecture du décodeur montrant les 3 sous-couches empilées. Attention particulière sur les flèches K, V qui viennent de l'encodeur vers la couche d'attention croisée. (Alammar: Transformer_decoder.png + transformer_decoding_1.gif)
Le masque causal en détail
Sans masque, la self-attention voit toute la séquence — passé et futur. Or à l'inférence, les mots futurs n'existent pas encore. Pour assurer la cohérence entre entraînement et inférence, on masque les positions futures :
Mask=0000−∞000−∞−∞00−∞−∞−∞0
On ajoute ce masque aux scores avant le softmax. Les −∞ deviennent des 0 après softmax → les mots futurs sont invisibles.
import numpy as np
def causal_mask(size):
"""Matrice triangulaire supérieure
remplie de -inf."""
mask = np.triu(
np.ones((size, size)) * float("-inf"),
k=1
)
return mask
print(causal_mask(4))
# [[ 0. -inf -inf -inf]
# [ 0. 0. -inf -inf]
# [ 0. 0. 0. -inf]
# [ 0. 0. 0. 0. ]]
En Keras : use_causal_mask=True dans MultiHeadAttention gère cela automatiquement.
Couche de sortie : Linear + Softmax
La sortie du dernier décodeur est un vecteur de dimension dmodel=512 pour chaque position. Pour produire un mot, on projette ce vecteur vers la taille du vocabulaire cible et on applique un softmax :
P(motj)=softmax(Wvocab⋅h+b)
Si le vocabulaire cible contient 30 000 mots, la couche linéaire est une matrice (512,30000). Le softmax transforme les logits en probabilités. On prend le mot avec la plus haute probabilité (greedy decoding) ou on utilise le beam search pour explorer plusieurs hypothèses en parallèle.
📌 IMAGE : Schéma montrant le vecteur de sortie du décodeur (512 dims) → couche linéaire → logits (30000 dims) → softmax → distribution de probabilité. Le mot avec la plus haute probabilité est sélectionné. (Alammar: transformer_decoder_output_softmax.png)
L'entraînement : Teacher Forcing et Cross-Entropy
Pendant l'entraînement, on ne génère pas mot par mot. Grâce au masque causal, on peut calculer la loss sur toute la séquence cible en une seule passe :
# Entrées d'entraînement pour "I am a student <eos>"
# decoder_input = ["<sos>", "I", "am", "a", "student"] (décalé de 1)
# decoder_target = ["I", "am", "a", "student", "<eos>"] (la vérité)
On fournit au décodeur les vrais mots décalés d'une position (technique appelée teacher forcing) et on compare la sortie prédite au mot attendu via la cross-entropy :
L=−∑t=1TlogP(yt∣y<t,X)
Le masque causal garantit que la prédiction du mot t ne dépend que des mots 1 à t−1, même si toute la séquence est présente dans le tenseur d'entrée. C'est ce qui permet la parallélisation massive de l'entraînement.
Récapitulatif
Tout mettre ensemble
L'architecture complète en un coup d'œil
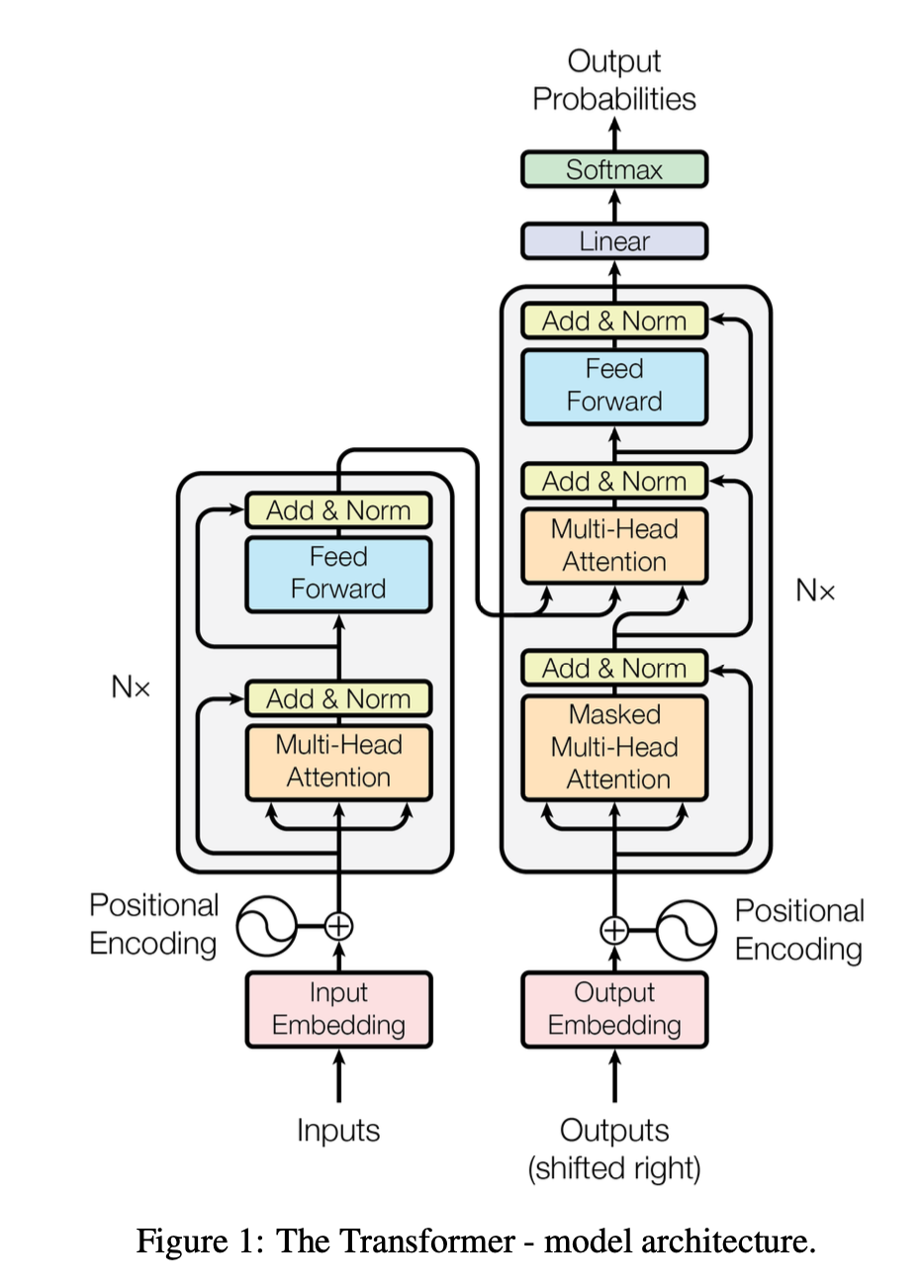
📌 IMAGE : Diagramme complet du Transformer original, style papier "Attention Is All You Need" Figure 1. Montrer les 6 encodeurs, 6 décodeurs, les connexions K/V, les embeddings + positional encoding des deux côtés, la couche linéaire + softmax finale.
Le flux des données :
Encodeur — Les tokens d'entrée sont convertis en embeddings, additionnés aux encodages positionnels, puis passent à travers 6 blocs identiques (self-attention + FFN). La sortie est un ensemble de représentations contextualisées de chaque mot source.
Décodeur — Les tokens cibles (décalés) suivent le même processus, mais avec une self-attention masquée. Ensuite, une attention croisée interroge les représentations de l'encodeur. Après 6 blocs, une couche linéaire + softmax produit la distribution sur le vocabulaire.
À l'inférence — Le décodeur génère un mot à la fois, en mode auto-régressif. Chaque mot prédit est réinjecté comme entrée pour le pas suivant.
Seq2Seq vs Attention vs Transformer
| Aspect | Seq2Seq (RNN) | Seq2Seq + Attention | Transformer |
|---|---|---|---|
| Encodeur | RNN séquentiel | RNN séquentiel | Self-attention parallèle |
| Contexte | Vecteur fixe unique | Somme pondérée dynamique | Self-attention + croisée |
| Parallélisation | Impossible (séquentiel) | Limitée (RNN) | Totale |
| Longues séquences | Dégradation rapide | Amélioration notable | Excellente (mais O(n2)) |
| Entraînement | Lent | Lent | Rapide (GPU/TPU) |
| Papier de référence | Sutskever 2014 | Bahdanau 2014 | Vaswani 2017 |
Pourquoi le Transformer domine aujourd'hui
Le Transformer est à la base de pratiquement tous les modèles de NLP modernes. BERT (2018) utilise uniquement la pile d'encodeurs pour des tâches de compréhension. GPT (2018→2024) utilise uniquement la pile de décodeurs pour la génération de texte. T5 et les modèles de traduction utilisent l'architecture complète encodeur-décodeur.
Au-delà du NLP, l'architecture s'est propagée à la vision (Vision Transformer / ViT), à l'audio, aux protéines (AlphaFold), à la robotique. Le mécanisme de self-attention est devenu le couteau suisse du deep learning.
La question de recherche active n'est plus "faut-il utiliser des Transformers ?" mais "comment les rendre plus efficaces ?" — d'où les travaux sur l'attention linéaire, les Transformers creux, les architectures Mamba/State Space Models, etc.
