Images et ConvNets
transfer learning
Pour aller plus loin
https://www.deeplearningbook.org/

Principaux types de réseaux
1. Feed Forward (Perceptron Multicouche)
Chaque neurone est connecté à tous les neurones de la couche suivante.
- Architecture la plus simple
- l'information circule dans une seule direction (entrée → couches cachées → sortie).
Cas d'utilisation: Classification, régression, reconnaissance de patterns simples.
Spécificités:
- Entraînement rapide
- Convient aux données tabulaires
RNN (Recurrent Neural Networks)
Réseaux avec connexions cycliques permettant de traiter des séquences temporelles.
- hidden state : Au lieu d'oublier chaque entrée après l'avoir traitée, un RNN maintient un état caché qui persiste et se met à jour à chaque étape.
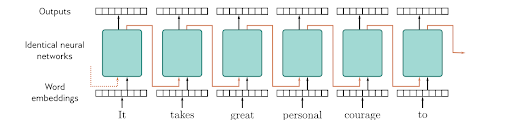
Cas d'utilisation: Traitement du langage naturel, prédiction de séries temporelles, génération de texte simple, traduction.
Spécificités:
- Vanishing gradient
- Variantes: LSTM et GRU pour améliorer la mémoire long-terme
- Entraînement plus coûteux en calcul
- Sensible à l'ordre des données
=> excelelnt post de Karpathy sur RNN
Transformers
- Architecture basée sur des mécanismes d'attention multi-têtes.
- Traite l'ensemble de la séquence en parallèle sans récurrence.
- Chaque token "voit" les autres tokens avec différents poids d'attention.
Cas d'utilisation: NLP (BERT, GPT), vision (Vision Transformers), génération, traduction, modèles de langage de grande taille.
Spécificités:
- Parallélisation complète (plus rapide à l'entraînement que RNN)
- Scalabilité massive (fonctionne bien avec énormément de données)
- Positional encoding pour capturer la position
- Coût mémoire élevé (attention O(n²))
- Nécessite de grands volumes de données pour bien performer
CNN (Convolutional Neural Networks)
- Utilise des convolutions au lieu d'une regression linéaire pour extraire des features locales.
- Réducteurs dimensionnels de l'information par pooling, idéals pour les données spatiales.
- Pooling: réduction dimensionnelle en extrayant les informations les plus importantes d'une région (max sur une zone de pixels).
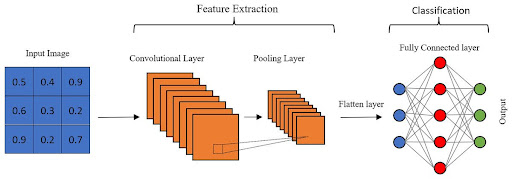
Cas d'utilisation: Vision par ordinateur, reconnaissance d'images, détection d'objets, segmentation sémantique.
Spécificités:
- Efficaces sur données bidimensionnelles (images)
- Partage de poids réduit les paramètres
- Hiérarchie de features : bas niveau → haut niveau
- Transfer learning très courant
Comparaison Rapide
| Aspect | Feed Forward | RNN | CNN | Transformer |
|---|---|---|---|---|
| Données | Tabulaires | Séquences | Images | Séquences/Texte |
| Parallélisation | Complète | Limitée | Bonne | Excellente |
| Mémoire | Aucune | Implicite | Locale | Globale (attention) |
| Complexité | Basse | Haute | Moyenne | Très haute |
| Données requises | Peu | Moyennes | Moyennes | Beaucoup |
Bref historique
- AlexNet (2012) - CNN, gagnant ILSVRC, relance la révolution du deep learning (15.3% d'erreur vs 26.2%)
- VGGNet (2014) - CNN, montre que la profondeur capture plus de complexité (16-19 couches empilées)
- Inception (2014) - CNN, gagnant ILSVRC, modules Inception parallèles (convolutions multiples simultanées)
- ResNet (2015) - CNN ultra-profond (152 couches), skip connections révolutionnaires
- Transformer (2017) - Architecture basée sur l'attention, remplace RNN/LSTM pour NLP, fondation des modèles modernes (BERT, GPT)
- Vision Transformer (2020) - Applique les transformers à la vision par ordinateur
- BERT (2018) - Transformer bidirectionnel pré-entraîné pour NLP
- GPT (2018+) - Transformer unidirectionnel pour génération de texte, base des LLMs modernes
Inception (2014)
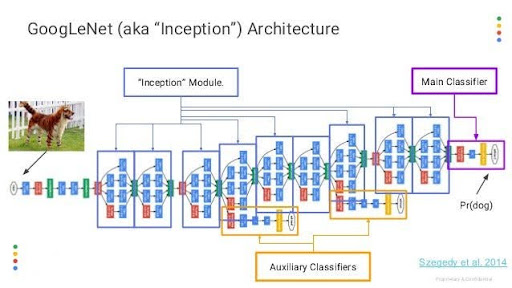
avec la relation suivante entre paramètres et FLOPs (Floating Point Operations):
FLOPs ~= 6 *Parameters * tokens
| Model | Parameters | Training FLOPs (approx) |
|---|---|---|
| GPT-2 (small) | 1.5B | 3 × 10^19 |
| GPT-3 | 175B | 3.14 × 10^23 |
| LLaMA-7B | 7B | ~1.4 × 10^21 |
| LLaMA-70B | 70B | ~1.4 × 10^22 |
Cycle de vie d'un modèle
Il y a 5 étapes:
- Définir le modèle : architecture
- Compiler le modèle : fonction de coût, optimiseur, métrique d'évaluation
puis comme en ML classique:
- Entraîner le modèle : définir le nombre d'epoch et le batch size
- Évaluer le modèle : calculer le score sur dataset de validation
- Inférence : faire des prédictions
CNN
MLP pas fantastique pour les images
- la couche Flatten fait perdre l'information spatiale
- le modèle va par exemple être sensible à la translation
pourtant si on bouge la chaise … ça reste une chaise !
Le CNN
capture l'information spatiale, les spécificités locales
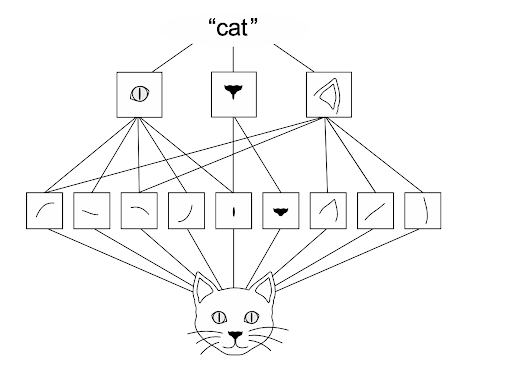
parfait pour :
- la classification d'images
- la segmentation d'images
- la détection d'objet
mais aussi les séries temporelles :
- numériques : simples et combinées
- reconnaissance de la parole
- classification audio
- analyse des capteurs (IoT)
CNN : principe de base
Décomposition de l'image de pixel en pixel, par petit carrés (3x3, 5x5)
- calcul de la convolution entre chaque carré et un filtre donné (tenseur rang 2 de dimension 3x3 ou 5x5, …). La valeur en sortie du calcul : un scalaire
- pooling : agréger ces valeurs en prenant le max ou la moyenne des valeurs (sous échantillonnage ou downsampling )
- enfin, envoyer le tout dans un MLP classique
Convolution
Filtrage des regions par un filtre (tenseur rang 2 de dimension 3x3 ou 5x5, …).
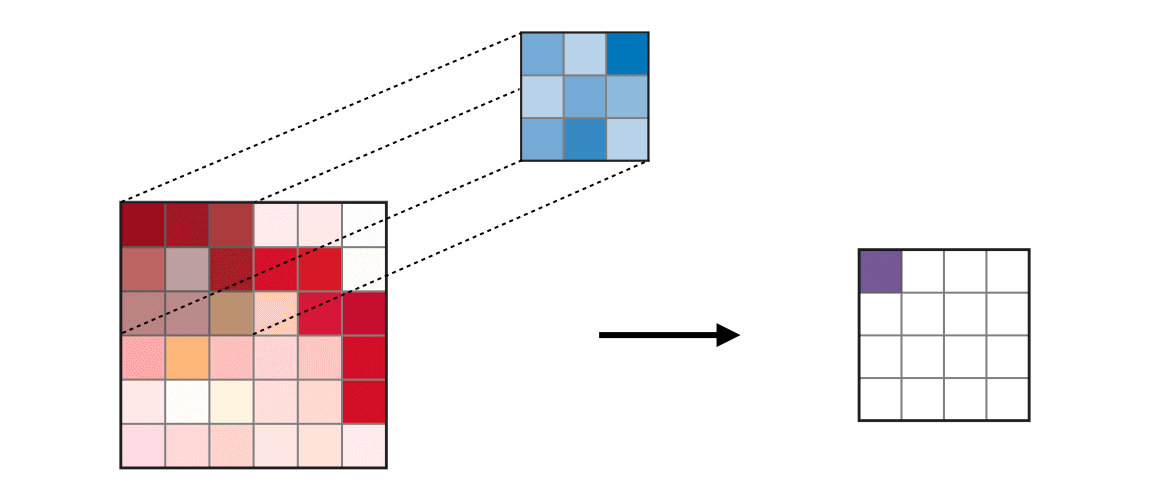
le calcul de "convolution"
- Dans les CNN, la "convolution" consiste à multiplier les éléments des matrices 2 à 2. C'est différent de la convolution en traitement du signal et des images qui retourne et décale le signal d'entrée.
Cependant le mot "convolution" est utilisé en raison du contexte historique, de la similarité conceptuelle, des considérations pratiques et de la cohérence terminologique.
L'idée principale reste la suivante : un noyau (filtre) est appliqué à une entrée (image) pour produire une carte de caractéristiques, qui capture les caractéristiques spatiales importantes de l'entrée.
Pooling
Reduction de dimension (downsampling) : max ou moyenne des valeurs sur une region (2x2, 3x3, 4x4, etc.)
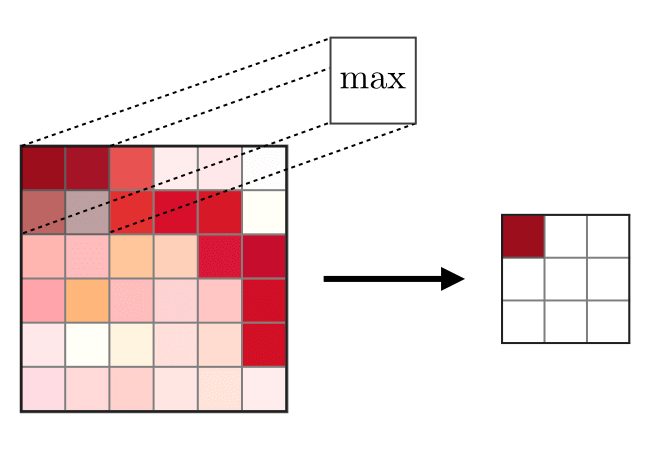
Voir le cours de Stanford sur les CNN
Apres la convolution vient le pooling aussi appelée sous-échantillonnage But :
- réduire la taille des données
- extraire les features importantes
- réduire la dépendance à la translation
2 techniques
- prendre le max (plus fréquent)
- prendre la moyenne

Le partie convolution et pooling réalise l'extraction des caractéristiques (features) de l'image d'entrée.
Les coefficients du filtre sont des paramètres d'apprentissage au même titre que les poids des noeuds dans une couche dense
Combiner plusieurs couches de convolution + pooling permet d'extraire des caractéristiques de plus en plus complexes
On peut enchaîner les couches de convolution sans avoir à chaque fois une couche de pooling
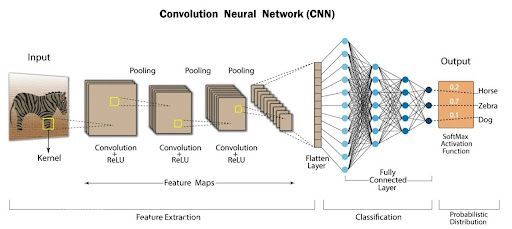
En resumé
- the first layers that consist of convolution + relu + pooling are simply to extract features
- and then the result of these first layers are fed into a classic feed forward
CNN Architecture Structure
Input Image
↓
[Conv + ReLU + Pooling] ← Feature Extraction (Layers 1-N)
[Conv + ReLU + Pooling] ← Hierarchical features
[Conv + ReLU + Pooling]
↓
Flatten (reshape to 1D vector)
↓
[Dense + ReLU] ← Classic Feed Forward
[Dense + ReLU] ← Classification/Regression
[Dense (output)]
↓
Prediction (class probabilities)
What Happens at Each Stage
Convolutional Layers (Feature Extraction):
- Early layers: detect simple features (edges, textures)
- Middle layers: detect mid-level features (corners, shapes)
- Deep layers: detect high-level features (objects, faces)
- Each layer builds on the previous one
Result: The image is progressively compressed into a high-level feature vector
Fully Connected Layers (Decision Making):
- Takes the flattened feature vector
- Acts like a classifier: "Given these features, what's the probability of each class?"
- This is just a regular multi-layer perceptron
Example (VGG-16)
Input: 224×224×3 image
↓
Conv blocks (13 layers): Extract features → 7×7×512
↓
Flatten: 7×7×512 = 25,088 neurons
↓
Dense layers (3 layers):
- Dense(4096) + ReLU
- Dense(4096) + ReLU
- Dense(1000) + Softmax → class prediction
The genius of CNNs is the separation of concerns:
- Conv layers learn WHAT features exist (spatial relationships)
- Dense layers learn HOW to combine features for decisions
Backprop in CNN
Backpropagation updates ALL layers, including the convolutional filters.
How it Works
Loss (final output error)
↓
Backprop through Dense layers
↓
Backprop through Flatten layer
↓
Backprop through Conv + ReLU + Pooling layers
↓
Update Conv Filter Weights ← gradient descent
What Gets Updated
During backpropagation:
Dense layers:
- Weights updated ✓
- Biases updated ✓
Convolutional layers:
- Conv filter weights updated ✓
- Conv biases updated ✓
- Pooling: NO weights (just selection operation)
- ReLU: NO weights (just gate)
Example
Initial Conv Filter (3×3):
[0.1 -0.2 0.3]
[0.5 0.0 -0.1]
[-0.2 0.4 0.1]
After 1 training step (backprop computes gradients):
[0.12 -0.19 0.31] ← Each weight adjusted
[0.51 0.01 -0.08]
[-0.18 0.42 0.12]
The gradient tells how much each weight contributed to the loss
In Practice
All layers are trainable by default:
- Conv filters learn to detect more useful features for YOUR task
- Dense layers learn better classification from those features
Oui! Plusieurs Filtres de Convolution
On a toujours plusieurs filtres en parallèle.
Exemple Concret
Input: Image 32×32×3 (RGB)
Cas 1 : UN SEUL filtre 3×3
Input: 32×32×3
Filtre: 3×3×3 (hauteur × largeur × canaux)
Paramètres du filtre:
3 × 3 × 3 = 27 paramètres (+ 1 bias) = 28 total
Output: 30×30×1 (une seule feature map)
Dans ce cas on n'extrait qu'une seule feature (par exemple "les bords verticaux"). Ce qui ne suffit pas
Cas 2 : 32 FILTRES en parallèle
Input: 32×32×3
32 filtres différents, chacun 3×3×3:
- Filtre 1: 3×3×3 = 27 params
- Filtre 2: 3×3×3 = 27 params
- ...
- Filtre 32: 3×3×3 = 27 params
Total: 32 × 27 = 864 paramètres (+ 32 bias) ≈ 896 total
Output: 30×30×32 (32 feature maps différentes!)
Chaque filtre apprend une feature différente:
- Filtre 1: détecte les bords verticaux
- Filtre 2: détecte les bords horizontaux
- Filtre 3: détecte les textures
- Filtre 4-32: autres patterns...
Visualisation
Input: 32×32×3
┌─────────────────┐
│ RGB Image │
└─────────────────┘
↓
[32 filtres en parallèle]
↓
┌──┬──┬──┬──┬─...─┐
│FM│FM│FM│FM│ │ ← 32 Feature Maps
└──┴──┴──┴──┴─...─┘
Chacun 30×30
↓
Output: 30×30×32
Comment ça change dans un Réseau Profond
VGG-16 Example:
Layer 1:
Input: 224×224×3
Filtres: 64 × (3×3×3) = 64 × 27 = 1,728 params
Output: 222×222×64
↓
Layer 2 (reçoit les 64 feature maps):
Input: 222×222×64
Filtres: 128 × (3×3×64) = 128 × 576 = 73,728 params ← BEAUCOUP plus!
Output: 220×220×128
↓
Layer 3:
Input: 220×220×128
Filtres: 256 × (3×3×128) = 256 × 1,152 = 294,912 params
Output: 218×218×256
Observation:
Couche 1: 1,728 params
Couche 2: 73,728 params (42× plus)
Couche 3: 294,912 params (170× plus!)
Pourquoi?
- Plus de filtres (64 → 128 → 256)
- Plus de canaux d'entrée (3 → 64 → 128)
Formule: params = (kernel_size² × input_channels × output_filters)
Formule Générale
Pour une couche Conv:
Paramètres = (Kernel_Height × Kernel_Width × Input_Channels × Output_Filters) + Output_Filters
Exemple:
- Kernel: 3×3
- Input channels: 64
- Output filters: 128
Params = (3 × 3 × 64 × 128) + 128 = 73,728 + 128 = 73,856
Résumé
| Aspect | Détail |
|---|---|
| Un filtre | 1 feature map en sortie |
| 32 filtres | 32 feature maps en sortie (32 features différentes détectées) |
| Paramètres croissent | Avec le nombre de filtres ET le nombre de canaux d'entrée |
| Plus profond | Chaque couche reçoit plus de canaux → explosion de paramètres |
Les multiples filtres en parallèle c'est la clé: c'est comme avoir plein de détecteurs différents qui travaillent en même temps! 🎯
Interet de multiplier les couches Conv - Pooling
Chaque set va extraire des caractéristiques de plus en plus complexes et générales
Premier ensemble de convolution + pooling :
- La couche de convolution initiale détecte des caractéristiques de bas niveau telles que les contours, les textures et les motifs simples.
- La première couche de pooling réduit les dimensions spatiales, en conservant les caractéristiques les plus importantes tout en réduisant les calculs et en atténuant le surapprentissage.
Deuxième ensemble de convolution + pooling :
- La deuxième couche de convolution s'appuie sur les caractéristiques détectées par la première couche, permettant au réseau de détecter des motifs plus complexes et des caractéristiques de niveau supérieur telles que les coins, les formes et les textures.
- La deuxième couche de pooling réduit encore les dimensions spatiales, permettant aux couches plus profondes de détecter des caractéristiques plus abstraites.
Pratique - notebook CNN
Sur le dataset Cats and Dogs
- construire un CNN à 1 puis à 2 Conv + Poolling
- Explorer différentes architectures
- monitorer l'entraînement avec tensorboard
- Augmenter le dataset
Tensorboard
https://www.tensorflow.org/tensorboard
Le tableau de bord Scalar montre comment le loss et les paramètres changent à chaque epoch. Vous pouvez également l'utiliser pour suivre la vitesse d'entraînement, le taux d'apprentissage et d'autres valeurs scalaires.
Le tableau de bord Graphs vous permet de visualiser votre modèle. Dans ce cas, le graphique Keras des couches s'affiche, ce qui peut vous aider à vous assurer qu'il est correctement construit.
Les tableaux de bord et Histogrammes montrent la distribution d'un Tensor au fil du temps. Cela peut être utile pour visualiser les poids et les biais et vérifier qu'ils changent de manière attendue.
techniques de reduction de l'overfit en deep learning
- Ajouter plus de couches convolutionnelles pour apprendre des caractéristiques plus complexes.
- Utiliser la batch normalisation pour stabiliser et accélérer l'entraînement. (BatchNormalization layer)
- Augmenter les données pour avoir plus de diversité dans le dataset d'entraînement
- Simplifier le modèle en réduisant le nombre de neurones dans les couches denses ou la taille des filtres de convolution.
- Ajouter de la régularisation L2 aux couches denses.
- Accroître le dropout, par exemple à 0,5 ou 0,6.
- Tune le learning rate.
- Accroître le batch_size et par conséquent le volume de données utilisé pour estimer le gradient
Augmenter les données
A chaque etape, le ImageDataGenerator prend un certain nombre (batch_size) d'images et les transforme aléatoirement (ou non)
De cette façon, le modèle voit des variations des images ce qui réduit l'overfitting
2 modes :
- création effective des images dans un répertoire
- à la volée : lorsque les images sont chargées, certaines sont transformées d'autres non
Les transformations possibles sont
- translation
- rotation
- Shear Transformation
- Zoom
- Brightness / luminosité
- symetrie verticale ou horizontale
- et Preprocessing
Pour aller plus loin : construire un pipeline input https://www.tensorflow.org/guide/data
BATCH SIZE
Le gradient qui sert à mettre à jour les poids du noeud lors de la rétropropagation est estimé à chaque fois sur une partie du dataset
le nombre d'échantillon estimé à chaque étape est appelé le batch size.
Valeurs courantes : N = 16, 32, 64, …
Le batch size est défini dans le train_generator, et le test_generator
train_generator = train_datagen.flow_from_directory(train_dir,
batch_size=20,
class_mode='binary',
target_size=(150, 150))
Comment régler le batch size ?
Augmenter le batch size
- itérations plus rapides (exploite les GPU)
- besoin de plus de mémoire
- meilleure estimation du gradient
- moins d'étapes
Réduire le batch size
- itérations plus lente
- besoin de moins de mémoire
- estimation du gradient plus variable
- plus de maj
Faut il réduire ou augmenter le batch size pour compenser l'overfit ?
D'un côté réduire le batch size réduit aussi l'overfit car :
- plus de bruit dans l'estimation du gradient
- donc moins tendance à coller aux données de training
Mais de l'autre côté augmenter le batch size réduit aussi l'overfit car:
- Meilleure estimation du gradient
- Effet de regularization
Approfondissement
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
Lire la partie architecture du cours de Stanford Convolutional Neural Networks https://cs231n.github.io/convolutional-networks/#architectures
Pour aller plus loin
L'excellent cours de stanford, notamment la section sur l'architecture https://cs231n.github.io/convolutional-networks/#architectures et ce cours récapitulatif https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-convolutional-neural-networks Le chapitre sur la convolution du Deep Learning book https://www.deeplearningbook.org/contents/convnets.html
Transfer Learning et fine tuning
le Fine tuning
En prenant pour départ un grand modèle déjà entraîné, l'idée est de réutiliser le modèle pour l'extraction des données
- on ne gèle que quelques unes des couches du modèle
- on ré-entraîne le modèle sur une nouveau dataset de taille conséquente
- avec un learning rate assez faible pour ne pas perdre la connaissance du modèle initial
Nécessite souvent beaucoup de données et des ressources informatiques puissantes
Transfer learning (plus facile)
En prenant pour départ un grand modèle déjà entraîné, l'idée est de réutiliser le modèle pour l'extraction des données
- on gèle les N-1 couches du modèle
- on supprime la dernière couche (celle de classification)
- on ré-entraîne seulement la dernière couche du modèle sur un jeux de donnée de taille réduite
- Les couches N-1 sont en fait utilisées pour l'extraction des features
Peu de données, faibles ressources informatiques
Transfer learning - 2 façon d'opérer
Workflow complet
- Charger un modèle pré-entraîné.
- Geler toutes les couches du modèle trainable = False.
- Ajouter une couche non gelée en sortie du modèle
- Entraîner votre nouveau modèle sur votre nouveau jeu de données.
Alternative plus légère
- Charger un modèle pré-entraîné.
- Faire passer votre nouveau jeu de données à travers ce modèle et enregistrer la sortie du modèle pré-entraîné.
- Utiliser cette sortie comme données d'entrée pour un nouveau modèle plus petit que vous entraînez. (MLP par exemple)
Dans ce cas vous ne faites passer le modèle de base sur vos données qu'une seule fois, plutôt qu'une fois par époque d'entraînement. Donc c'est beaucoup plus rapide et moins coûteux.
Combiner les modèles keras
inner_model = Sequential([
layers.Input(shape=(10,)),
layers.Dense(32, activation='relu'),
layers.Dense(16, activation='relu')
])
outer_model = Sequential([
inner_model, # Include the inner model as a layer
layers.Dense(64, activation='relu'),
layers.Dense(1, activation='sigmoid')
])
# Compile the outer model
outer_model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
Transfer learning
On va utiliser le modèle InceptionV3 : Total params: 21802784 (83.17 MB) + 311 layers!!!
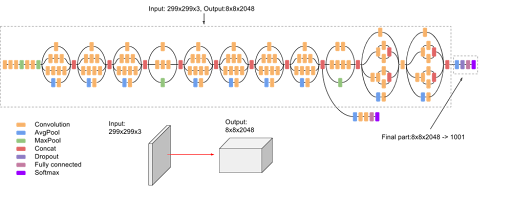
Inception V3
- Introduit en 2015
- Les modules Inception combinent des convolutions de 1x1, 3x3, et 5x5 et des pooling layers dans une même couche ce qui capture des caractéristiques à différentes échelles.
- L'architecture inclut également des couches factorisées, des couches de réduction de dimensionnalité et des connexions résiduelles.
- InceptionV3 a été entraîné sur le dataset ImageNet, comprenant des millions d'images réparties en 1000 classes.
- environ 24 millions de paramètres.
- Des techniques comme le batch normalization et la régularisation sont utilisées pour améliorer la stabilité et la performance du réseau.