Logistic regression

• pourquoi la regression logistique s'appelle 'regression' alors que l'on veut faire de la classification
• evaluer la performance d'un modele de classification binaire
  • histogram des probabilités
  • matrice de confusion
  • ROC-AUC
  • autres metriques : precision, recall, F1 score
• classification binaire ou multiclass: one vs rest / one vs one
• dataset désequilibré : sous échantillonnage, sur echantillonage, SMOTE

voir aussi slides

---

Régression Logistique

classification

---

Régression logistique – classification - ML

• Classification ≠ Regression
• Logistic Regression
• fonction logit
• Confusion Matrix
• AUC – score F1
• régression logistique avec scikit-learn
• prédicteurs catégoriels
  • encodage dummy
  • encodage binaire
• Datasets déséquilibrés
• Classification multiclasse
  • un contre tous (one vs rest)
  • un contre un (one vs one)

---

Classification binaire : la variable cible est catégorielle

La sortie de la régression linéaire est continue

Si nous utilisons la régression linéaire pour classifier des animaux (chat = 0, lapin = 1, chien = 2), nous avons besoin de seuils arbitraires qui ne reflètent pas la réalité

Pourquoi aurions-nous un ordre arbitraire entre les animaux ?

• chats < lapins < chiens a-t-il plus de sens que
• Chiens < chats < lapins

De plus, la plage de sortie de la régression linéaire n'est pas contrainte ou limitée..

On ne peut pas utiliser la régression linéaire pour la classification

---

Régression logistique

L'idée principale derrière la classification binaire avec la régression logistique

Objectif : Classification binaire : 0 / 1

1. Utiliser la régression linéaire
2. Contraindre les valeurs estimées Y entre l'intervalle [0, 1]
3. Interpréter les résultats comme une probabilité P d'appartenir à l'une des catégories (0 ou 1)
4. Définir un seuil Tau = 0.5
5. Classifier avec la règle :
   • si P < Tau => Y appartient à la catégorie 0
   • sinon P > Tau => Y appartient à la catégorie 1

---

Fonction logistique

de R -> [0,1]

f(x) = 1/(1 + e^(-x))

---

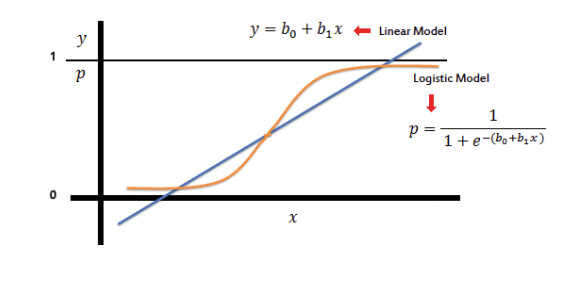
Régression logistique vs Régression linéaire

Modèle linéaire : y = b₀ + b₁x

Modèle logistique : p = 1/(1 + e^(-(b₀ + b₁x)))

---

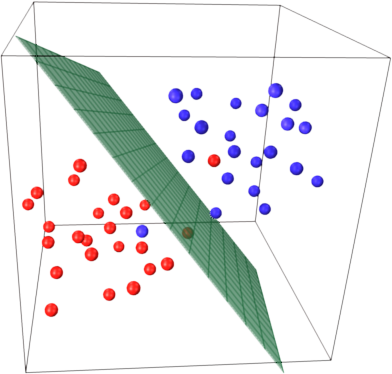
Trouver le meilleur hyperplan qui sépare les données

2D : ŷ = a_1 x_1 + a_0

3D : ŷ = a_1 x_1 + a_2 x_2 + a_0

---

Dataset de défaut de crédit

disponible ici

Prédicteurs :

• continus : balance, income
• binaire : student

Variable cible :

• default indique qu'une personne a fait défaut sur ses paiements
• default est une variable binaire qui prend les valeurs 0 ou 1
  • Non (0) 500
  • Oui (1) 333

import statsmodels.formula.api as smf
import pandas as pd

# Charger le dataset
df = pd.read_csv('credit_default_sampled.csv')

# instancier le modèle
model = smf.logit('default ~ income + balance', data = df)

# Ajuster le modèle aux données
results = model.fit()

# Résultats
results.summary()

---

Résultat de régression logistique

default ~ income + balance

• R-squared
• F-statistique
• t-statistique

---

avec scikit learn

modele logistic regression

import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

# Charger le dataset
df = pd.read_csv('credit_default_sampled.csv')

# Préparer les features et la cible
X = df[['income', 'balance']]
y = df['default']

# Optionnel mais recommandé : standardiser les features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Diviser en ensemble d'entraînement et de test (optionnel)
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=42, stratify=y
)

# Instancier le modèle
model = LogisticRegression(max_iter=1000)

# Ajuster le modèle aux données
model.fit(X_train, y_train)

# Obtenir les coefficients et l'intercept
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

# Score du modèle
print("Score d'entraînement:", model.score(X_train, y_train))
print("Score de test:", model.score(X_test, y_test))

# Prédictions
y_pred = model.predict(X_test)
y_proba = model.predict_proba(X_test)

---

Histogramme des probabilités

L'histogramme des valeurs estimées fournit une bonne indication du pouvoir de séparation du modèle.

y_proba = results.predict(df[['income', 'balance']])

• Modèle médiocre : très confus
• Modèle excellent : séparation claire
  • p < 0.5 : Défaut : Non
  • p > 0.5 : Défaut : Oui

---

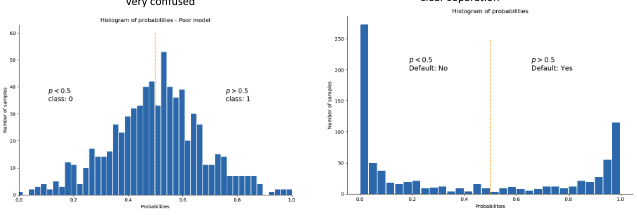
Classes prédites en fonction des probabilités de prédiction

# sortie des prédictions du modèle sous forme de probabilités, yhat dans [0,1]
y_proba = results.predict(df[['income', 'balance']])

# transformer les probabilités en classe
predicted_class = (y_proba > 0.5).astype(int)

print(predicted_class)
> [1,1,1,1...,0,0,0]

Note que le choix du seuil de classification (0.5) reste arbitraire.

---

Matrice de confusion

4 cas possibles

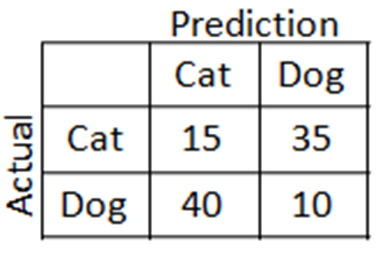
2 corrects :

• 1 classifié comme 1
• 0 classifié comme 0

2 faux :

• 1 classifié comme 0
• 0 classifié comme 1

	Prédit 1	Prédit 0
Réel 1	Vrais Positifs	Faux Négatifs
Réel 0	Faux Positifs	Vrais Négatifs

results.pred_table()

---

Matrice de confusion : default ~ income + balance

	Défaut Prédit	Non-Défaut Prédit
Défaut Réel	286	47
Non-Défaut Réel	40	460

Sur 333 échantillons de défaut :

• 286 ont été correctement prédits comme défaut par notre modèle (Vrais positifs)
• 47 ont été incorrectement prédits comme non-défaut par notre modèle (Faux Négatifs)

Et sur 500 échantillons non-défaut :

• 460 ont été correctement prédits comme non-défaut par notre modèle (Vrais Négatifs)
• 40 ont été incorrectement prédits comme défaut par notre modèle (Faux Positifs)

---

Métriques de classification

Nous pouvons définir plusieurs métriques en utilisant la matrice de confusion

• Précision (Accuracy) = (VP + VN) / (P + N)

• Taux de Vrais Positifs = (VP) / (VP + FP)

• Taux de Faux Positifs = (FP) / (VP + FP)

• nombre d'échantillons correctement classifiés : 460 + 286 = 746

• nombre total d'échantillons : 833

• donc notre précision est 746 / 833 = 89.56%

• TPR = 286 / 333 = 85.89%

• FPR = 47 / 333 = 14.11%

---

Matrice de confusion - (le nom est approprié)

de la page Wikipedia Confusion Matrix

---

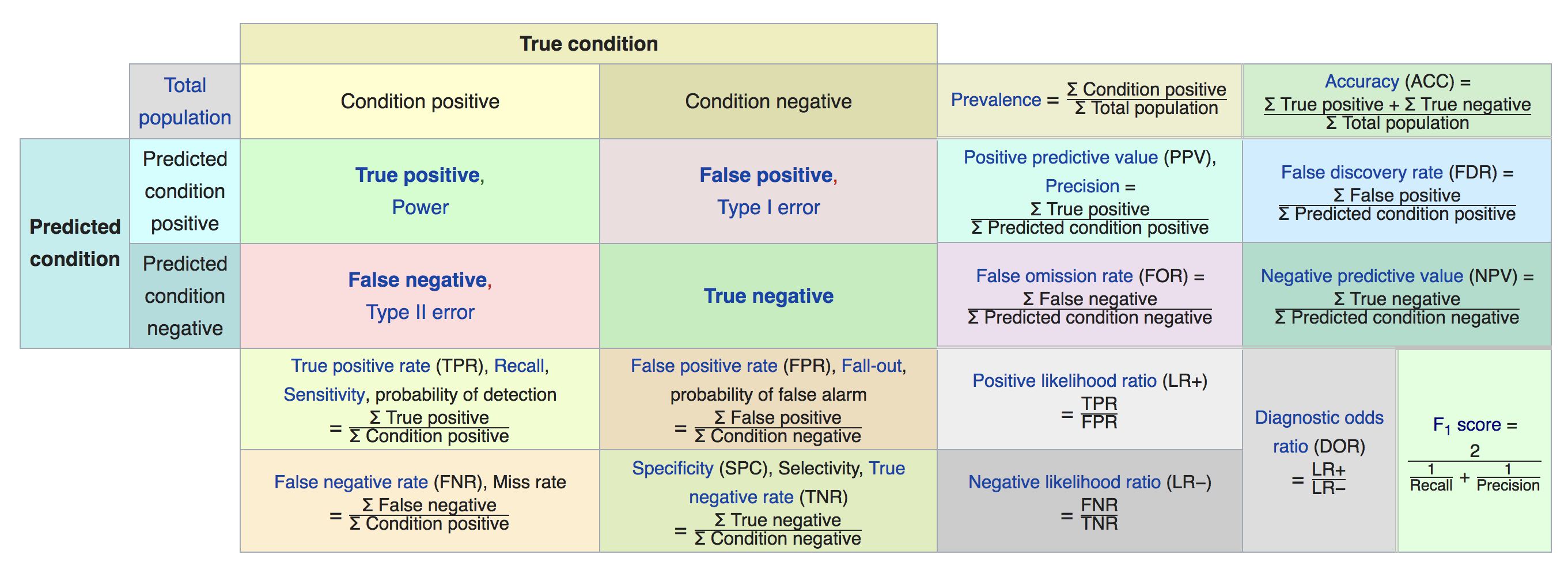
À votre tour – default ~ income + balance + student

Construire le modèle : default ~ income + balance + student

1. instancier le modèle smf.logit
2. Ajuster le modèle
3. interpréter les résultats
4. calculer la matrice de confusion
5. calculer la précision, TPR, FPR
6. tracer l'histogramme des probabilités

---

Et le seuil ?

Que se passe-t-il si nous utilisons un seuil de classification différent ?

La matrice de confusion et les métriques associées changent également.

t = 0.5

• Acc (0.5) = 746 / 833 = 89.56%
• TPR = 286 / 333 = 85.89%
• FPR = 47 / 333 = 14.11%

t = 0.75

• Acc (0.75) = (243 + 481)/888 = 81%
• TPR = 243 / 333 = 72.97%
• FPR = 90 / 333 = 27.03%

---

ROC-AUC

Tracer la courbe TPR vs FPR en faisant varier le seuil de 0 à 1 donne la courbe ROC.

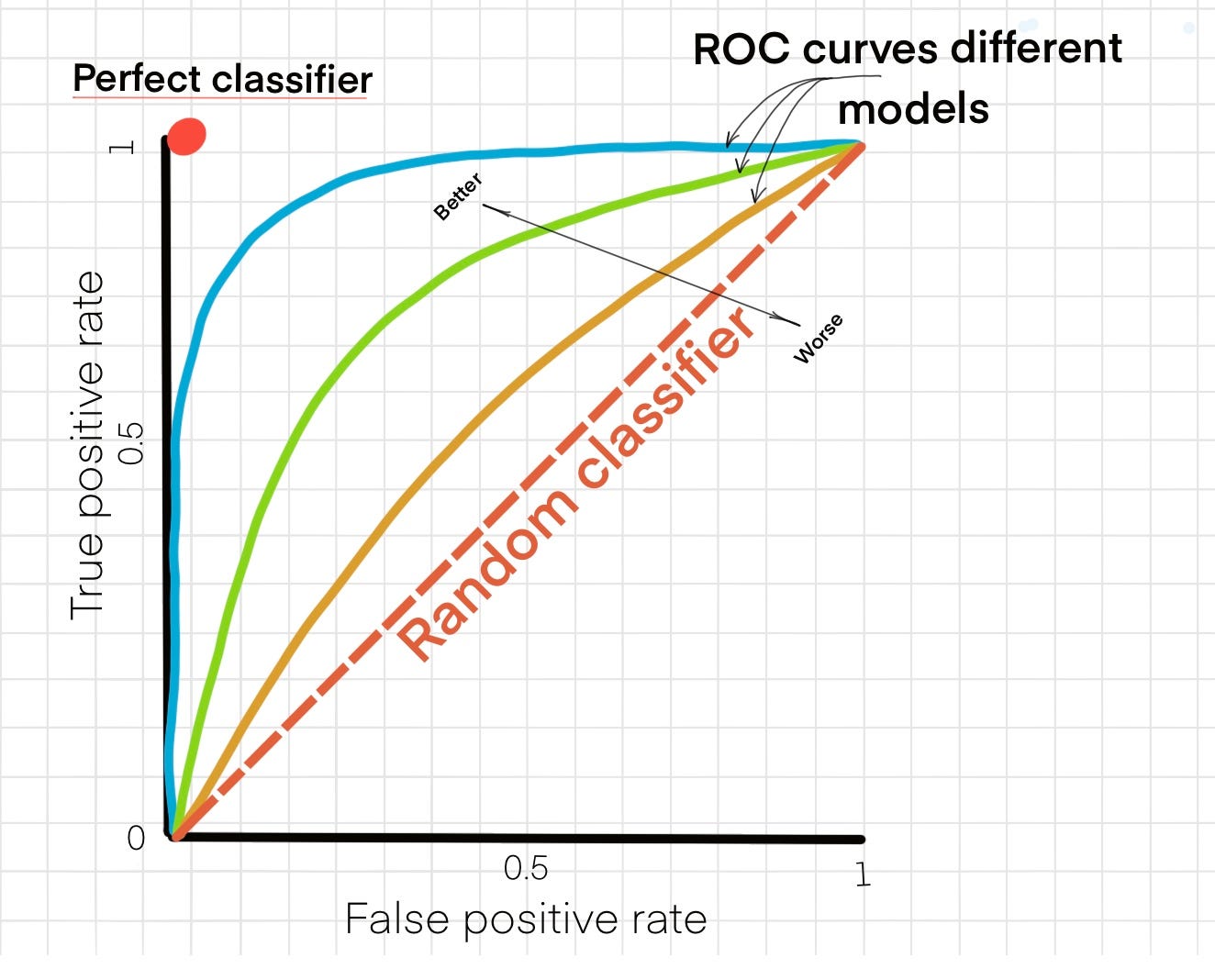
L'aire sous la courbe (AUC) est une métrique plus robuste que la précision.

yhat = results.predict(df)

from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(df['default'], yhat)

from sklearn.metrics import roc_auc_score
score = roc_auc_score(df['default'], yhat)

---

À votre tour – default ~ income + balance + student

Pour le modèle default ~ income + balance + student :

• Construire le modèle
• Interpréter les résultats
• Calculer la matrice de confusion
• Calculer la précision, TPR et FPR
• Calculer l'AUC
• Tracer la courbe ROC

Comparer avec le modèle default ~ income.

---

Datasets déséquilibrés

---

Le paradoxe de la précision

Le dataset original de défaut de crédit contient :

• 333 cas de défaut
• 9667 cas de non-défaut

Un modèle (stupide, inutile) qui prédit toujours non-défaut a une précision de 96.67%.

La classe cible est une forte minorité. Le dataset est déséquilibré.

Quatre stratégies pour gérer le déséquilibre de classe :

• Sous-échantillonnage de la classe majoritaire
• Sur-échantillonnage de la classe minoritaire
• Combinaison de sur- et sous-échantillonnage
• SMOTE

---

Équilibrer les classes

Stratégies pour résoudre le problème du déséquilibre de la classe minoritaire

• sous-échantillonner la classe majoritaire
• sur-échantillonner la classe minoritaire

On peut aussi

• mélanger les 2 approches : sur et sous-échantillonnage

Le but n'est pas de balancer parfaitement les classes 50 / 50

---

À vous – dataset déséquilibré

Sur le dataset complet de défaut de crédit :

• Construire le modèle default ~ income + balance + student.
• Calculer la précision et l'AUC, et tracer la courbe ROC.

Puis :

• Sur-échantillonner la classe minoritaire.
• Sous-échantillonner la classe majoritaire.
• Varier les ratios.

# sur-échantillonner la classe minoritaire
df = pd.read_csv('credit_default.csv')
minority = df[df.default == 0].sample(n = 2000, replace = True)
majority = df[df.default == 1]

data = pd.concat([minority, majority])
# mélanger
data = data.sample(frac = 1)

---

SMOTE

L'algorithme SMOTE est implémenté en sélectionnant aléatoirement l'un des échantillons de données de classes peu nombreuses, puis en sélectionnant plusieurs de ses données d'échantillons voisins par interpolation linéaire.

L'algorithme SMOTE génère des échantillons artificiels en trois étapes :

1. sélection d'un échantillon aléatoire peu nombreux.
2. Sélectionner une instance parmi ses K voisins de classe minoritaire les plus proches.
3. Enfin, un nouvel échantillon est créé en interpolant aléatoirement deux échantillons

---

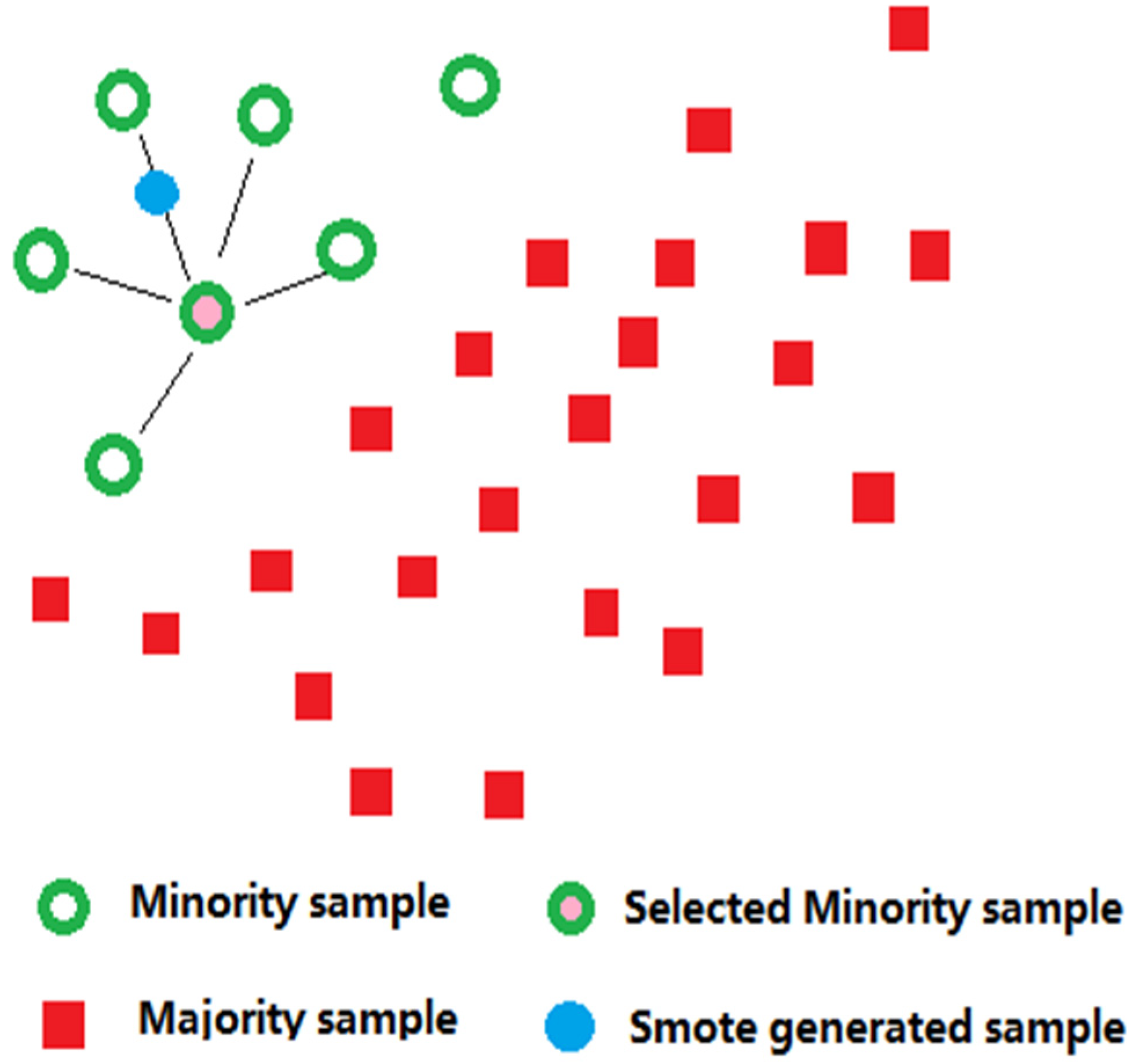
SMOTE ne fonctionne pas !

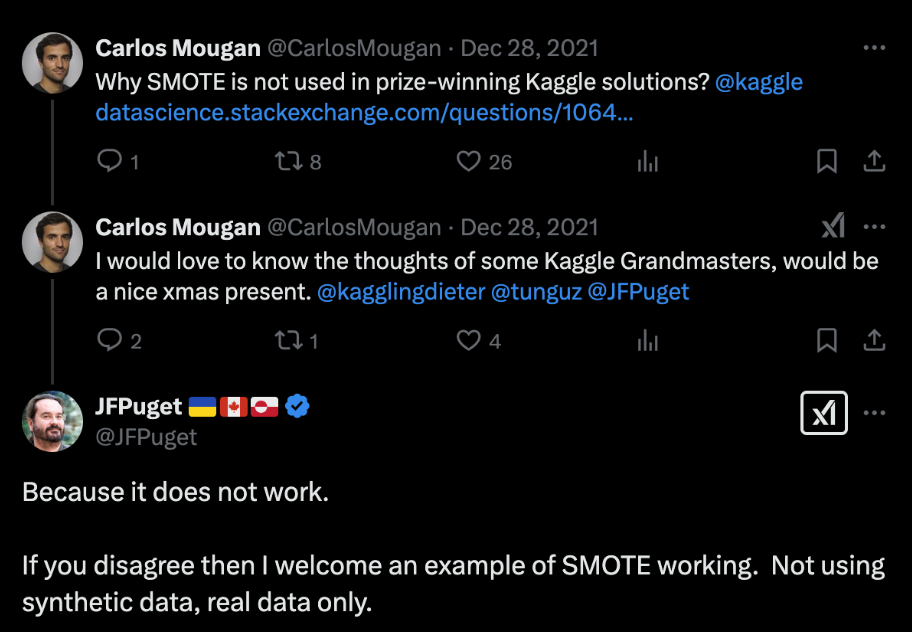
"Parce que cela ne fonctionne pas.

Si vous n'êtes pas d'accord, alors bienvenue avec un exemple de SMOTE fonctionnant. N'utilisant pas de données synthétiques, uniquement des données réelles."

---

Imbalanced learn

Un package Python pour s'attaquer à la malédiction des datasets déséquilibrés dans l'apprentissage automatique http://imbalanced-learn.org

Voir aussi Conseils pour gérer les données déséquilibrées dans l'apprentissage automatique

---

Encodage des variables catégorielles

---

Encodage des variables catégorielles

Encodage one-hot – Encodage dummy

Comment convertir les variables catégorielles en variables numériques ?

Binaire :

• Oui/Non
• 1/0
• Homme/Femme
• Spam/Légitime
• Action : Acheter, Sauvegarder, Se connecter

Multinomial, non-ordinal :

• Liste de villes, pays, destinations, groupes d'âge
• Niveau d'éducation
• Marques de voitures

Exemples

Marque de voiture : Audi, Renault, Ford, Fiat

Si un nombre arbitraire est attribué à chaque marque, une hiérarchie est créée :

• Audi → 1, Renault → 2, Ford → 3, Fiat → 4

De même :

• Chien, chat, souris, poulet → {1,2,3,4}
• Pourquoi un poulet serait-il quatre fois un chien ?

Parfois, attribuer un nombre à chaque catégorie a du sens—catégories ordonnées :

• Enfant, jeune, adulte, personne âgée → {1,2,3,4}
• Négatif, neutre, positif → {-1, 0, 1}

---

Prédicteurs catégoriques – encodage dummy

Charger auto-mpg

Origin (3) et name (nombreux) sont des catégories non ordonnées (non-ordinales). Comment inclure origin comme prédicteur dans un modèle linéaire ?

Avec Pandas, créer une variable par catégorie :

• American : 0 ou 1
• European : 0 ou 1
• Japanese : 0 ou 1

N-1 nouvelles variables sont nécessaires pour N catégories.

origin_variables = pd.get_dummies(df.origin)
df = df.merge(origin_variables, left_index=True, right_index=True)
results = smf.ols('mpg ~ Japanese + European', data = df).fit()

# Essayer
results = smf.ols('mpg ~ Japanese + European + American', data = df).fit()

pd.get_dummies() crée N-1 variables. Puis, définir le modèle : mpg ~ American + European

---

Prédicteurs catégoriques – statsmodel

Statsmodels encode directement les variables catégorielles avec

mpg ~ C(origin)

---

Interprétation des coefficients - catégories

La moyenne par catégorie

df[['mpg','origin']].groupby(by = 'origin').mean().reset_index()

mpg ~ C(Origin)

• Intercept = mpg_American
• origin[T.European] = mpg_European − mpg_American
• origin[T.Japanese] = mpg_Japanese − mpg_American

---

Prédicteurs catégoriques

Comment inclure la marque de voiture dans auto-mpg ? Il y a 36 catégories. Certaines catégories ont peu d'échantillons.

Encodage binaire !

import category_encoders as ce
# définir l'encodeur
encoder = ce.BinaryEncoder(cols=['brand'])
df = encoder.fit_transform(df)

Au lieu de

• mpg ~ brand

Nous utilisons le modèle

• mpg ~ brand_0 + brand_1 + … + brand_5

---

Encodage binaire

https://towardsdatascience.com/all-about-categorical-variable-encoding-305f3361fd02/

Nombre de variables binaires = INT( log2(Nombre de catégories))

---

Category encoders - la bibliothèque

https://contrib.scikit-learn.org/category_encoders/index.html

Un ensemble de transformateurs de style scikit-learn pour encoder les variables catégorielles en numérique avec différentes techniques.

---

Classification multiclasse - Multinomiale

---

Classification multinomiale

One vs One

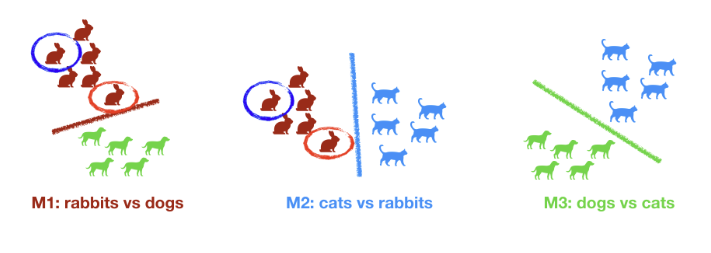
Pour N catégories on construit N modèles Le modèle final est obtenu par vote ou par moyenne

M1 : lapins vs chiens M2 : chats vs lapins M3 : chiens vs chats

---

Classification multinomiale

One vs Rest

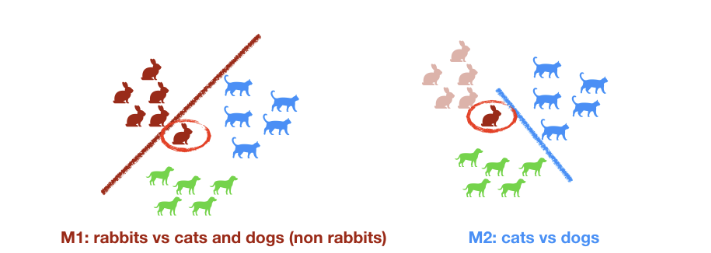
N-1 modèles sont nécessaires propagation de l'erreur

M1 : lapins vs chats et chiens (non lapins) M2 : chats vs chiens

---

Pratique

sur un google colab

Construire un modèle de régression logistique scikit-learn sur le dataset des pingouins

voir aussi la page Kaggle pour le dataset Pingouins sur Kaggle

• charger les données dans un dataframe pandas

• transformer les valeurs catégorielles en valeurs numériques

• utiliser une stratégie un contre tous (one vs rest) ou un contre un (one vs one)

• en utilisant le meilleur modèle

  • sélectionner les meilleurs régresseurs, y en a-t-il que vous pouvez supprimer
  • évaluer la performance du modèle
  • tracer la distribution des probabilités pour chaque classe et évaluer la performance du modèle
  • quels échantillons ne sont pas correctement classifiés
  • la régression logistique est-elle un bon modèle ?