Réseaux de neurones

Perceptron, Fast forward

Contenu

Quelques dates

Article : Réseaux de neurones sur Wikipedia

A la base, le neurone

Équivalent à une régression linéaire + activation

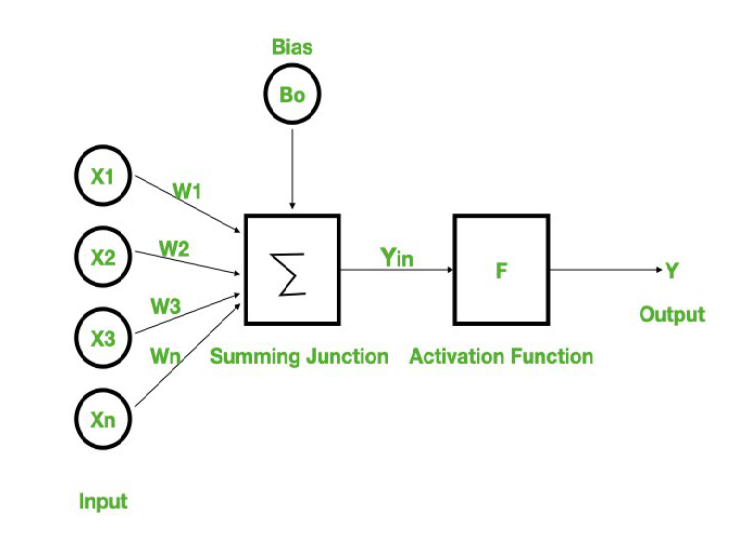
neurone schema 
y = F(x_1 .w_1 + x_2.w_2 + ... + x_N.w_N + b)

Fonction d'activation

Analogie faible avec les neurones du cerveau;

Capacité à apprendre des relations non linéaires à partir d'une relation lineaire.

Le choix de la fonction d'activation va influencer le comportement du reseaux et notamment contraindre sa tendance à exploser (exploding gradient) ou à disparaitre (vanishing gradient). Et surtout sa rapidité de calcul.

source

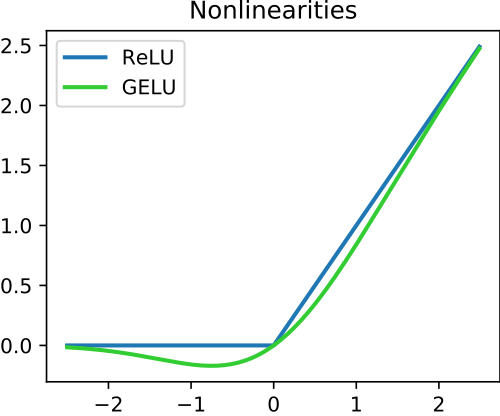
RELU & GELU

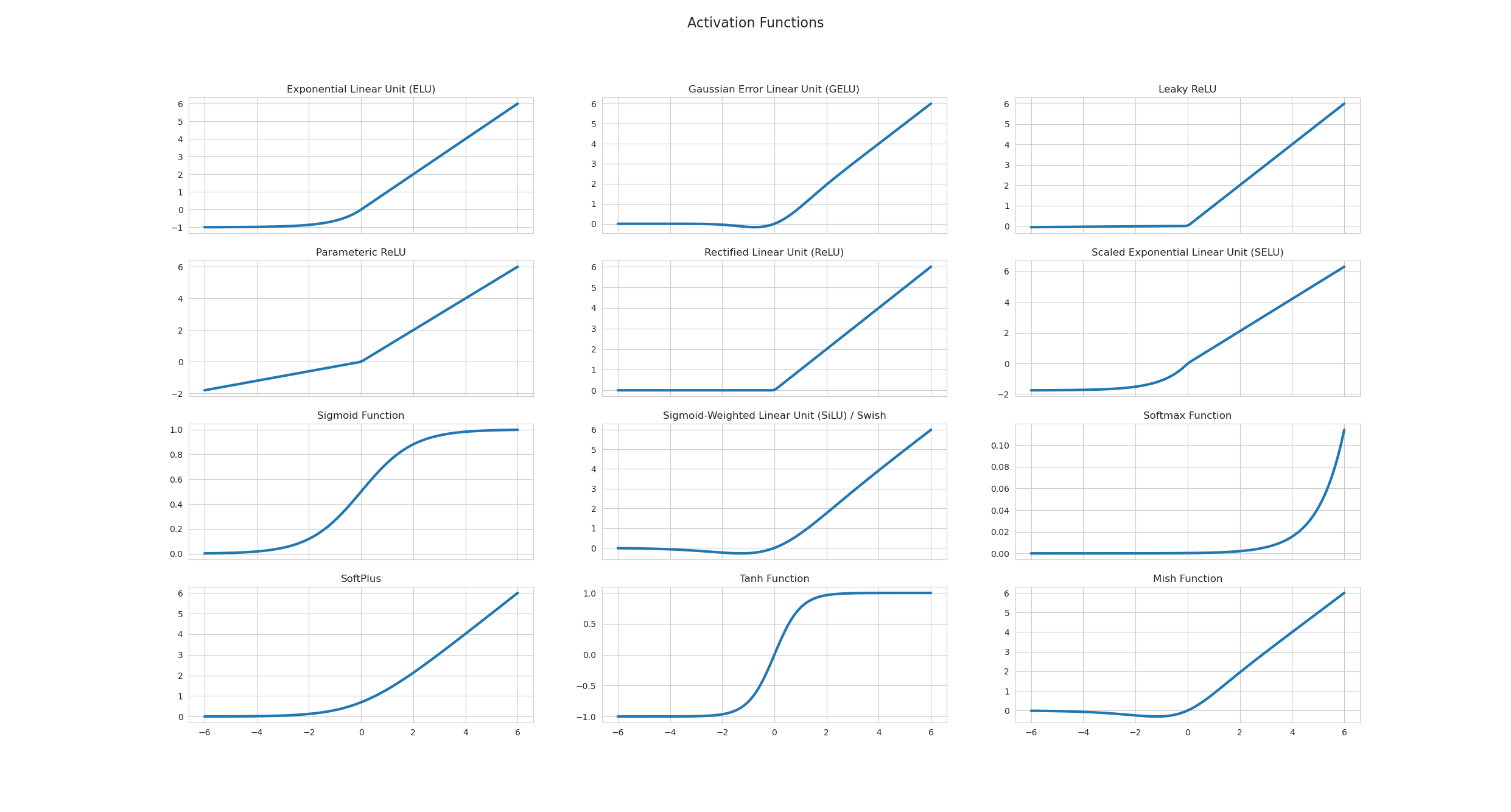
More activation functions

fonctions d'activation

Le perceptron

input : data, learning_rate

weights = random()
bias = 0

FOR each iteration DO
    FOR each sample IN data DO
        z = weights · sample.features + bias
        prediction = 1 if z > 0 else 0
        error = sample.label - prediction
        weights = weights + learning_rate * error * sample.features
        bias = bias + learning_rate * error

Contexte d'une classification binaire linéairement séparable

en python

import numpy as np

# Données
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
# Example linearement separable
y = np.array([1, 0, 1, 0])

# XOR : non linearement separable
# y = np.array([0, 1, 1, 0])

# Initialisation
coefs = np.zeros(2)
bias = 0
taux_apprentissage = 0.2

# Entraînement
for epoch in range(20):
    # pour chaque échantillon (choisi aléatoirement)
    for idx in np.random.choice(len(X), len(X)):
        x = X[idx]

        #  produit scalaire + biais => output de la regression lineaire
        valeur = np.dot(x, coefs) + bias

        # fonction activation (heavyside)
        prediction = 1 if valeur > 0.5 else 0


        # le perceptron n'apprend que de ses erreurs
        # mettre a jour coefs / biais si prediction != vraie valeur
        if prediction != y[idx]:
            erreur = y[idx] - prediction
            coefs += taux_apprentissage * erreur * x
            bias += taux_apprentissage * erreur

        print("epoch", epoch, prediction == y[idx], "coefs", coefs, "bias", bias)

limites du percetron une couche

Inadapté à la non linéarité.

Pour apprendre des fonctions non linéaires, des architectures de réseaux de neurones plus avancées sont utilisées.

Par exemple

Different shades of Le percetron

Single cell (1 neurone):

Single layer avec plusieurs cellules:

Exemple : 3 neurones pour reconnaître A, B, C

Multi-layer:

XOR vs AND

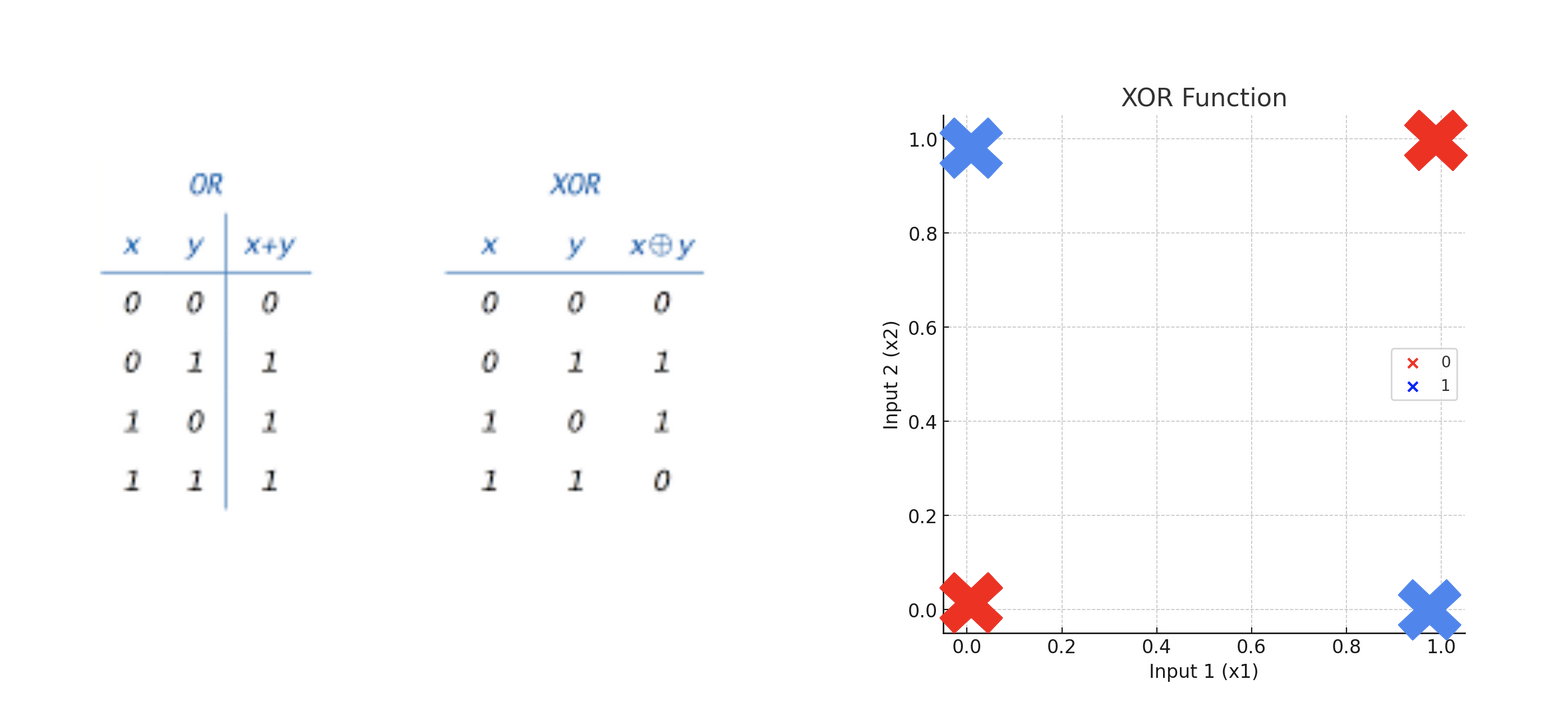
xor or and

XOR / AND - Notebook

Notebook: XOR vs AND

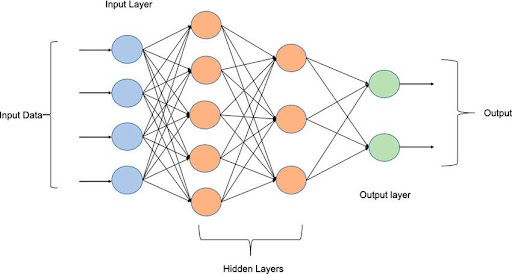
Multi layer perceptron

mlp

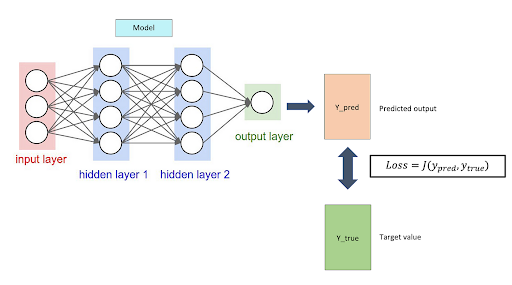
Fonction de cout

pour mettre a jour les poids / coefficients des cellules, on utilise une fonction de cout (loss function).

nn loss function

MLP — Propriétés

MLP avec scikit-learn

mlp sklearn

MLPClassifier

learning rate :

optimisation :

et

solvers:

Backpropagation

nécessaire pour adapter les coefficients des noeuds en fonction de l'erreur et du résultat de la fonction de coût

pass forward

backward

C'est comme pour le gradient descent, mais en plusieurs couches.

Impact de la derivee de la fonction d'activation sur la vitesse d'apprentissage

gradient = dérivée

Pour un neurone unique

Considérons un neurone simple avec :

Lors de la backpropagation, on veut calculer comment ajuster le poids w pour minimiser l'erreur. Pour cela, on a besoin de ∂L/∂w le gradient (aka la dérivée) de la loss function L par rapport à w.

w_{t+1} = w_{t} - learning_rate * ∂L/∂w

En utilisant la règle de dérivation en chaîne :

∂L/∂w = ∂L/∂y × ∂y/∂z × ∂z/∂w

Or :

Donc : ∂L/∂w = ∂L/∂y × f'(z) × x

Sans f'(z), on ne peut pas calculer le gradient ! La dérivée agit comme un "multiplicateur" qui module l'amplitude du gradient qui se propage.

Pour une couche complète

Pour une couche avec plusieurs neurones, chaque neurone i a sa propre sortie y_i = f(z_i).

Le gradient qui arrive de la couche suivante (∂L/∂y) doit être propagé vers la couche précédente. Pour chaque neurone i de la couche :

∂L/∂z_i = ∂L/∂y_i × f'(z_i)

La dérivée f'(z_i) détermine donc :

  1. L'amplitude de propagation : Si f'(z_i) ≈ 0 (zones saturées de sigmoid/tanh), le gradient devient presque nul → problème de "vanishing gradient"

  2. La direction d'ajustement : Le signe de f'(z_i) influence si on augmente ou diminue les poids

  3. La vitesse d'apprentissage locale : Une grande valeur de f'(z_i) amplifie le gradient, permettant des ajustements plus importants

gradient qui arrive depuis la couche suivante

exemple sur architecture simple à 3 couches

Imaginons un réseau très simple :

Entrée (x) → Couche 1 → Couche 2 → Couche 3 (sortie) → Perte (L)

Avec les notations :

Le flux de la backpropagation: La backpropagation calcule les gradients en partant de la fin (de la perte) et en remontant vers le début :

L ← y₃ ← y₂ ← y₁ ← x

Étape 1 : On part de la perte

D'abord, on calcule ∂L/∂y₃ (comment la perte change quand la sortie finale change)

= dérivée de la fonction de cout / y₃

Étape 2 : On remonte à la couche 2

Pour mettre à jour les poids de la couche 2, on a besoin de ∂L/∂y₂

Mais la perte L ne dépend pas directement de y₂. Elle dépend de y₂ à travers y₃ :

L dépend de y₃
y₃ dépend de y₂
Donc L dépend de y₂

Par la règle de la chaîne :

∂L/∂y₂ = ∂L/∂y₃ × ∂y₃/∂y₂

∂L/∂y₃ est le "gradient qui arrive depuis la couche suivante" (couche 3)

Pourquoi "arrive depuis la couche suivante" ?

Quand on est à la couche 2 et qu'on veut calculer nos gradients locaux :

  1. On ne recalcule pas tout depuis la perte L
  2. On reçoit ∂L/∂y₂ qui a déjà été calculé par la couche 3
  3. Ce gradient nous dit : "Si tu changes ta sortie y₂ d'une petite quantité, voici comment ça affectera la perte finale L"

Code conceptuel

# Forward pass
y1 = couche1(x)
y2 = couche2(y1)
y3 = couche3(y2)
L = perte(y3, cible)

# Backward pass
grad_y3 = ∂L/∂y3  # Calculé directement depuis la perte = dérivée de la fonction de Loss

# Pour la couche 2
grad_y2 = grad_y3 × ∂y3/∂y2  # Le gradient "arrive" de la couche 3
# Maintenant on peut utiliser grad_y2 pour mettre à jour les poids de couche2

# Pour la couche 1
grad_y1 = grad_y2 × ∂y2/∂y1  # Le gradient "arrive" de la couche 2

C'est cette propagation en cascade des gradients qui donne son nom à la "back-propagation" : les gradients se propagent de l'arrière vers l'avant du réseau.

Exemple avec des chiffres : a-step-by-step-backpropagation-example

Fonctions d’activation

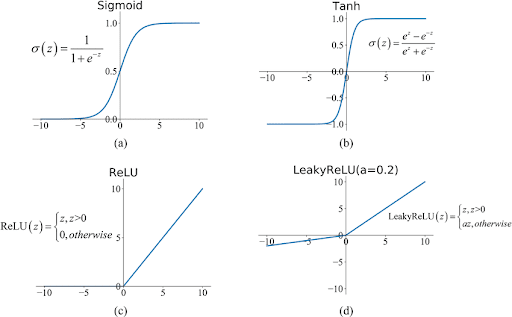
fonctions activations

Chaque fonction introduit une non-linéarité différente qui impact la vitesse d'apprentissage et la convergence.

Certaines fonctions ont des zones "mortes" (dead zone) où rien n'est plus appris (ReLU : zone négative)

Sigmoid

ReLU (Rectified Linear Unit)

Tanh

Softmax

Leaky ReLU

Zones mortes

Les zones mortes en ReLU = les neurones ne s'entraînent plus

def ReLU(x):
    return max(0, x)

Donc si un neurone reçoit toujours des valeurs négatives :

La solution :

vanishing gradient

Le probleme avec la sigmoide et la tanh est que le gradient est très petit aux extrémités.

Comme on multiple par la derivée en x de couche en couche il y a propagation de la multiplication par une valeur petite => la maj devient super petite et le gradient disparaît

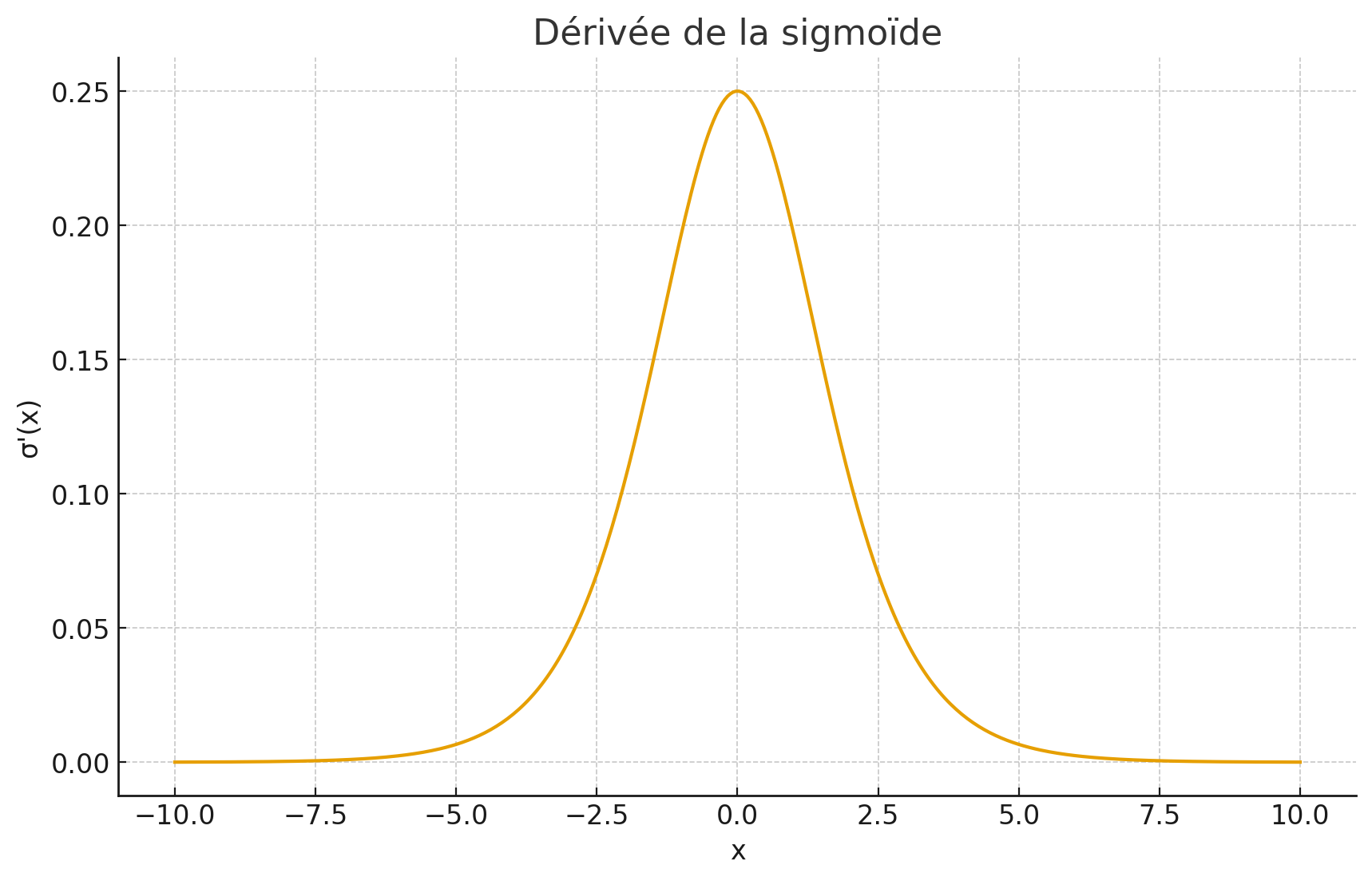
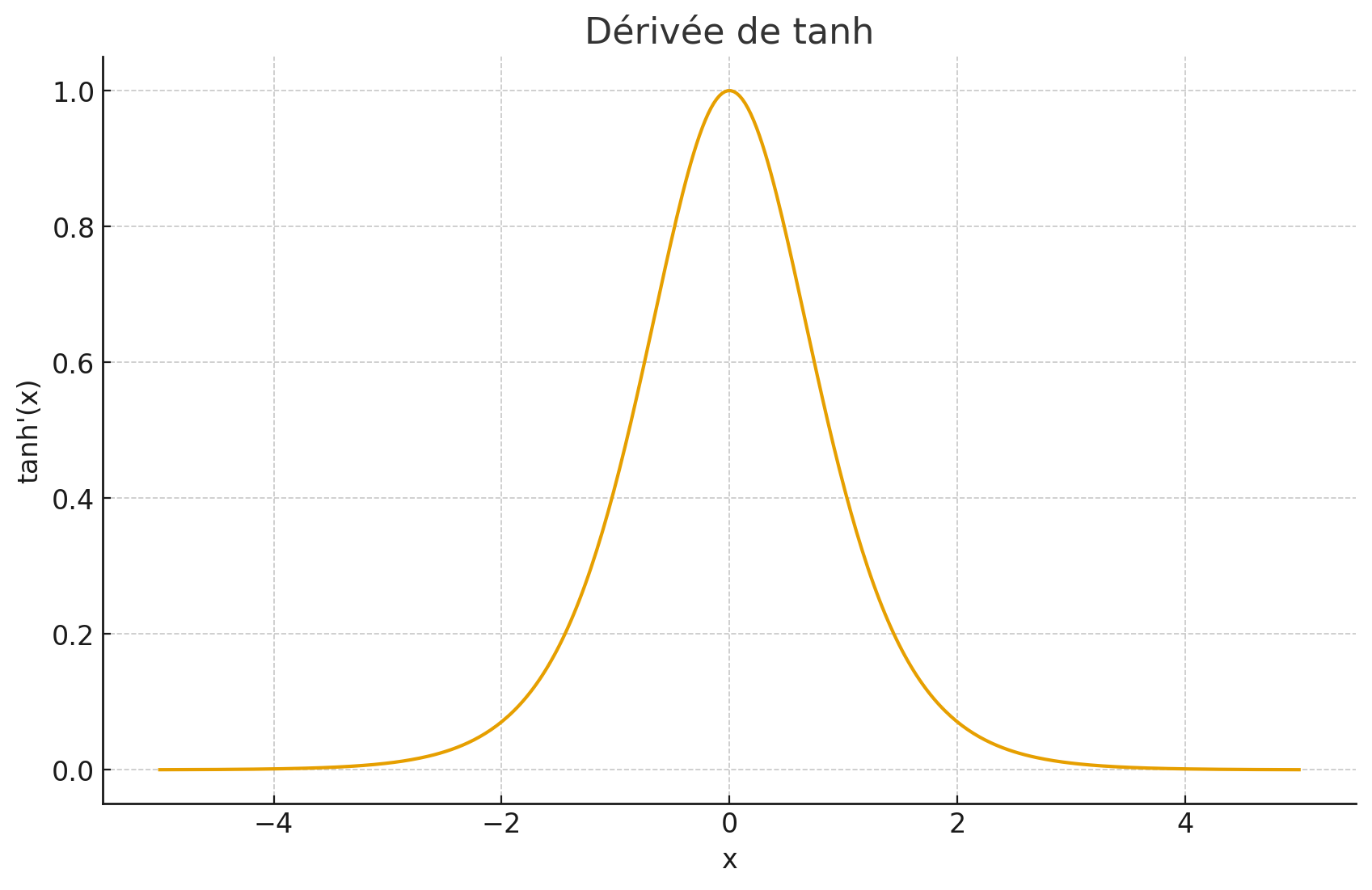
derivee sigmoide derivee sigmoide

Vanishing Gradient = les gradients deviennent de plus en plus petits en remontant dans le réseau.

Pourquoi avec Sigmoid ?

Sigmoid a une dérivée max de 0.25. Quand on a plusieurs couches :

Couche 1: gradient = 0.25
Couche 2: gradient = 0.25 * 0.25 = 0.0625
Couche 3: gradient = 0.0625 * 0.25 = 0.015625
Couche 4: gradient = 0.015625 * 0.25 = 0.004

Chaque couche multiplie par 0.25, ça devient exponentiellement petit.

Problème:

Exemple visuel:

Sortie: gradient = 0.5
Couche cachée 5: 0.5 * 0.25 = 0.125
Couche cachée 4: 0.125 * 0.25 = 0.03
Couche cachée 3: 0.03 * 0.25 = 0.007
Couche cachée 1: ~ 0.000001  ← QUASI MORT

Solutions:

C'est pourquoi ReLU domine aujourd'hui ! 🎯

Exploding gradient

Inversement on a le probleme des gradients qui explosent

Le problème de l'exploding gradient

Gradient final = gradient_initial × f'(z₁) × W₁ × f'(z₂) × W₂ × ... × f'(zₙ) × Wₙ

Si ces valeurs sont grandes (ex: |W| > 1 et f'(z) ≈ 1), après 10 couches :

Conséquences concrètes :

Techniques de remédiation du exploding gradient

On "coupe" les gradients trop grands quand ils depassent un certains seuil. Simple et efficace

if |gradient| > seuil:
    gradient = +/- seuil

Voir aussi

Optimizers (solvers)

Les solvers = optimiseurs qui ajustent les poids pendant l'entraînement.

SGD (Stochastic Gradient Descent)

Momentum

RMSprop

Adam ⭐ (le plus frequent)

Différences principales:

SolverVitesseStabilitéMémoire
SGDLentTrès stableFaible
MomentumRapideStableFaible
RMSpropRapideBonFaible
AdamTrès rapideTrès bonMoyen

Comment choisir ?

Règle simple: Adam d'abord, puis ajuste si besoin !

Atelier MLP — MNIST

Refs:

Régularisation : limiter l’overfit sans ajouter de biais

Ajouter une contrainte pour empêcher le modèle de coller trop aux données d’entraînement.

Contraintes possibles :

Arbres de décision :

Régularisation des réseaux de neurones

Dropout

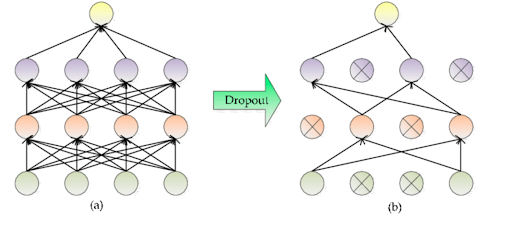
nn dropout

Batch normalization

En pratique: Dropout + Early Stopping = 90% du travail !

Resume

Suite

Tenseurs, Keras, ...

1 / 0