Arbres de Décision
Overfit et biais
Random Forests
Decision Trees
Qu’est-ce qu’un arbre de décision ?
- Structure hiérarchique pour la prise de décision
- Série de questions binaires (oui/non)
- Chaque nœud = une règle de décision
- Chaque feuille = une prédiction
Avantages
- Interprétable et visualisable
- Pas besoin de normalisation des données
- Gère les relations non-linéaires
2. Exemple Simple : Classification
Contexte
Prédire si un client va acheter un produit
Features possibles
- Âge du client
- Revenus annuels
- Nombre de visites sur le site
- Temps passé sur la page produit
Arbre résultant
Si revenus > 50k€
└─ Si âge > 35
└─ Achète (85% de probabilité)
└─ Sinon
└─ N'achète pas (70% de probabilité)
Sinon
└─ N'achète pas (90% de probabilité)
3. Classification avec Scikit-learn
Dataset synthétique
# Créer un dataset de classification
X, y = make_classification(
n_samples=1000,
n_features=20,
n_informative=15,
n_redundant=5,
random_state=42
)
# Séparer train/test
X_train, X_test, y_train, y_test = split_data(X, y, test_size=0.2)
4. Application d’un Decision Tree
Entraînement sans contraintes
# Créer et entraîner le modèle
tree_model = DecisionTreeClassifier(
max_depth=None, # Pas de limite
min_samples_split=2,
min_samples_leaf=1
)
tree_model.fit(X_train, y_train)
# Évaluation
train_score = tree_model.score(X_train, y_train)
test_score = tree_model.score(X_test, y_test)
Résultats typiques
- Train accuracy: 100%
- Test accuracy: 75%
- Problème évident d’overfitting!
5. Visualisation de l’Overfitting
Symptômes observables
- Arbre très profond (15-20 niveaux)
- Nombreuses feuilles avec 1-2 échantillons
- Décisions très spécifiques au training set
- Écart important train/test performance
Pourquoi ?
- Le modèle “mémorise” le bruit
- Règles trop spécifiques
- Manque de généralisation
6. Contraindre la Profondeur
Limitation de la complexité
# Arbre avec profondeur limitée
tree_constrained = DecisionTreeClassifier(
max_depth=5,
min_samples_split=20,
min_samples_leaf=10
)
tree_constrained.fit(X_train, y_train)
Nouveaux résultats
- Train accuracy: 85%
- Test accuracy: 82%
- Meilleure généralisation!
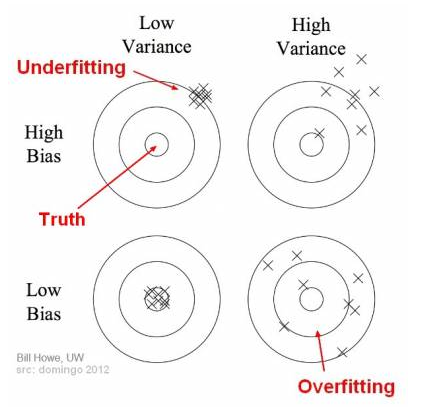
7. Overfitting et Bias
Overfitting (Surapprentissage) - Variance
- Le modèle apprend le bruit des données
- Excellente performance sur train set
- Mauvaise performance sur test set
- High variance, low bias
Underfitting (Sous-apprentissage) - Biais
- Erreur systématique
- Le modèle est trop simple
- Mauvaise performance même sur train set
- Manque de généralisation
- Manque de flexibilité
8. Détection de l’Overfitting
Méthodes de détection
Gap train/test
- Si
train_score - test_score > 0.1→ Overfitting probable
Courbes d’apprentissage (learning curve)
On fait varier la taille du training set
train_scores = []
val_scores = []
for size in [100, 200, 500, 1000]:
model.fit(X_train[:size], y_train[:size])
train_scores.append(model.score(X_train[:size], y_train[:size]))
val_scores.append(model.score(X_val, y_val))
plot(train_scores, val_scores)
Demo
9. Stratégies de Remédiation
Pour réduire l’overfitting
1. Régularisation (pour les arbres)
max_depth: Limiter la profondeurmin_samples_split: Minimum pour divisermin_samples_leaf: Minimum par feuillemax_features: Limiter les features considérées
2. Plus de données
- Augmenter la taille du dataset
- Data augmentation si possible
3. Ensemble methods
- Random Forests
- Gradient Boosting
10. Random Forests - Vue d’ensemble
Concept principal
Combiner plusieurs arbres de décision pour:
- Réduire l’overfitting
- Améliorer la généralisation
- Maintenir la performance
Principe du “Wisdom of Crowds”
- Chaque arbre vote
- La majorité l’emporte (classification)
- La moyenne est calculée (régression)
Bootstrap
Principe
- Créer N échantillons avec remise
- Chaque échantillon = même taille que l’original
Avantages
- Plus de données
- Plus de flexibilité
- Plus de généralisation
Bootstrap = sampling avec remise
- même si chaque échantillon bootstrap est différent, quand on fait la moyenne de TOUS les échantillons possibles, on retombe exactement sur la moyenne de nos données originales. C’est pour ça que ça ne biaise pas nos prédictions.”
Un sac avec 5 billes numérotées [1,2,3,4,5]. Si tu tires une bille, notes son numéro, la remets, et répètes ça 1000 fois, la moyenne de tous tes tirages sera ~3 (la moyenne originale). C’est exactement ce que fait le bootstrap avec les données.
=> petit scrit python pour illustrer
11. Comment ça marche ?
Bootstrap Aggregating (Bagging)
- Bootstrap sampling
- Créer N échantillons avec remise
- Chaque échantillon = même taille que l’original
- Entraîner N arbres
- Un arbre par échantillon bootstrap
- Chaque arbre voit des données différentes
- Random feature selection
- À chaque split, considérer seulement m features
- Typiquement: m = √(total_features)
- Agrégation
- Classification: vote majoritaire
- Régression: moyenne
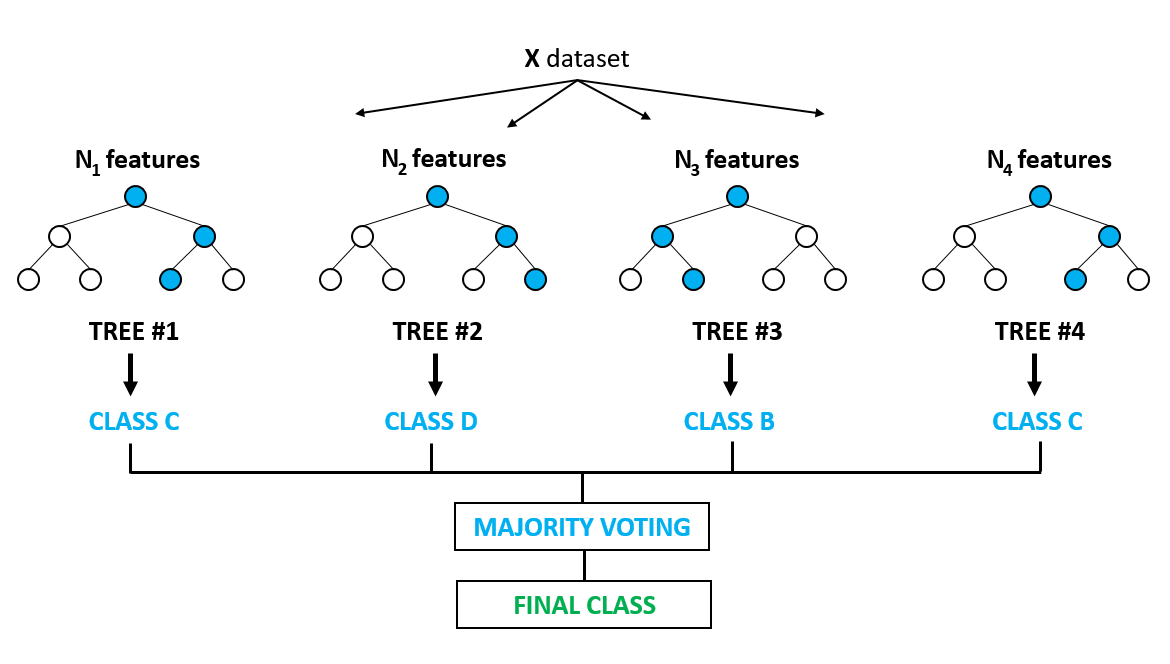
Dans le bagging classique (comme Random Forest), on utilise des learners qui OVERFITTENT (arbres profonds non contraints), PAS des weak learners avec high bias.
1. Bagging avec des modèles qui overfittent (CLASSIQUE)
- Modèles utilisés : Arbres profonds (max_depth=None), low bias, HIGH VARIANCE
- Problème ciblé : Réduction de la VARIANCE
- Mécanisme : Moyenner des modèles très variables réduit la variance
- Exemple : Random Forest
2. Bagging avec des weak learners (MOINS COMMUN)
- Modèles utilisés : Arbres peu profonds (max_depth=2-3), HIGH BIAS, low variance
- Problème ciblé : Peut aider un peu avec le bias ET la variance
- Mécanisme : La diversité des bootstrap samples peut capturer différents aspects
- Exemple : Mon script de démonstration
Pourquoi la confusion ?
Le bagging peut techniquement améliorer les deux, MAIS :
# Cas 1: OPTIMAL pour bagging - High variance models
tree_overfit = DecisionTreeClassifier(max_depth=None) # ← Random Forest utilise ça!
# Variance: HIGH → bagging très efficace
# Bias: LOW → reste low après bagging
# Cas 2: SOUS-OPTIMAL pour bagging - High bias models
tree_weak = DecisionTreeClassifier(max_depth=2) # ← Weak learner
# Variance: LOW → peu à gagner du bagging
# Bias: HIGH → bagging ne peut pas beaucoup réduire
La théorie mathématique :
Pour un ensemble de M modèles :
- Bias(ensemble) ≈ Bias(modèle individuel) → Le bagging ne réduit PAS le bias
- Var(ensemble) = ρσ² + (1-ρ)σ²/M → Le bagging réduit FORTEMENT la variance
Implications pratiques :
Random Forest (le vrai bagging)
# Utilise des arbres PROFONDS qui overfittent
RandomForestClassifier(
max_depth=None, # Pas de limite !
min_samples_split=2, # Peut créer des feuilles très spécifiques
min_samples_leaf=1 # Maximum overfit
)
→ Chaque arbre overfit horriblement, mais l’ensemble généralise bien !
Boosting (différent du bagging)
# Utilise des WEAK learners avec high bias
AdaBoostClassifier(
base_estimator=DecisionTreeClassifier(max_depth=1), # Stumps!
)
→ Combine séquentiellement des weak learners pour réduire le BIAS
Résumé :
| Méthode | Type de base learner | Réduit quoi ? | Exemple |
|---|---|---|---|
| Bagging | Modèles complexes (overfit) | VARIANCE | Random Forest |
| Boosting | Weak learners (underfit) | BIAS | AdaBoost, XGBoost |
Dans votre cours, je recommande de clarifier :
- Random Forest = bagging d’arbres PROFONDS (pas des weak learners!)
- Le bagging réduit principalement la variance, pas le bias
- Mon script de démo avec weak learners est pédagogique mais pas optimal
Le bagging est plus efficace avec des modèles instables à haute variance qu’avec des weak learners !
12. Paramètres Principaux random forests
Hyperparamètres clés
n_estimators
- Nombre d’arbres dans la forêt
- Plus = meilleur (jusqu’à un plateau)
- Défaut: 100
max_features
- Features à considérer par split
- ‘sqrt’, ‘log2’, ou nombre/fraction
- Trade-off: diversité vs performance individuelle
max_depth
- Profondeur maximale des arbres
- None = arbres complets (peut overfitter)
min_samples_split / min_samples_leaf
- Contrôle la taille minimale des nœuds
- Plus élevé = arbres plus simples
Demo Colab
13. Pratique sur Dataset Standard
Exemple avec Iris ou Wine dataset
# Charger les données
X, y = load_wine_dataset()
X_train, X_test, y_train, y_test = split_data(X, y)
# Créer le Random Forest
rf_model = RandomForestClassifier(
n_estimators=100,
max_depth=None,
max_features='sqrt',
random_state=42
)
# Entraîner
rf_model.fit(X_train, y_train)
# Évaluer
train_score = rf_model.score(X_train, y_train)
test_score = rf_model.score(X_test, y_test)
Impact du max_features
Analyse de sensibilité
max_features_values = [1, 2, 'sqrt', 'log2', None]
results = {}
for mf in max_features_values:
rf = RandomForestClassifier(
n_estimators=100,
max_features=mf
)
rf.fit(X_train, y_train)
results[mf] = {
'train': rf.score(X_train, y_train),
'test': rf.score(X_test, y_test),
'overfit_gap': train - test
}
Insights
- Peu de features → Plus de diversité, moins d’overfitting
- Toutes les features → Arbres similaires, risque d’overfitting
16. Impact de max_depth
Test de profondeur
depths = [2, 5, 10, 20, None]
for depth in depths:
rf = RandomForestClassifier(
n_estimators=100,
max_depth=depth
)
evaluate_model(rf, X_train, X_test, y_train, y_test)
Trade-offs
- Arbres peu profonds:
- ✅ Moins d’overfitting
- ❌ Possible underfitting
- Arbres profonds:
- ✅ Capture de patterns complexes
- ❌ Risque d’overfitting (mais réduit par le bagging)
17. Out-of-Bag (OOB) Score
Validation gratuite
- ~37% des échantillons ne sont pas dans chaque bootstrap
- Ces échantillons “out-of-bag” servent de validation
rf = RandomForestClassifier(
n_estimators=100,
oob_score=True
)
rf.fit(X_train, y_train)
print(f"OOB Score: {rf.oob_score_}")
print(f"Test Score: {rf.score(X_test, y_test)}")
Avantage
- Pas besoin de validation set séparé
- Estimation non-biaisée de la performance
18. Feature Importance
Mesurer l’impact des variables
rf.fit(X_train, y_train)
importances = rf.feature_importances_
# Visualiser
for feature, importance in zip(feature_names, importances):
print(f"{feature}: {importance:.3f}")
# Top features
top_features = sorted(zip(feature_names, importances),
key=lambda x: x[1],
reverse=True)[:5]
Utilité
- Sélection de features
- Interprétabilité du modèle
- Réduction de dimensionnalité
19. Comparaison: Decision Tree vs Random Forest
Performance typique
| Métrique | Decision Tree | Random Forest |
|---|---|---|
| Train Accuracy | 100% | 95% |
| Test Accuracy | 75% | 88% |
| Overfitting Gap | 25% | 7% |
| Stabilité | Faible | Élevée |
| Temps d’entraînement | Rapide | Plus lent |
| Interprétabilité | Excellente | Moyenne |
20. Points Clés à Retenir
Decision Trees
✅ Simple et interprétable ✅ Pas de preprocessing nécessaire ❌ Tendance forte à l’overfitting ❌ Instable (petits changements → grands impacts)
Random Forests
✅ Réduit significativement l’overfitting ✅ Performance généralement excellente ✅ Robuste et stable ❌ Plus lent et gourmand en ressources ❌ Moins interprétable (boîte noire)
Stratégie pratique
- Commencer avec Random Forest par défaut
- Si besoin d’interprétabilité → Decision Tree contraint
- Toujours valider avec cross-validation
- Surveiller le gap train/test
strategie d’otpimisation des parametres
Stratégie Principale : NE PAS commencer par max_depth !
Random Forest a besoin d’arbres qui overfittent (high variance) pour que le bagging fonctionne bien.
Ordre recommandé :
- n_estimators (le plus important) - Chercher le plateau de performance
- max_features (contrôle la diversité) - ‘sqrt’ est souvent optimal
- min_samples_split/leaf (réglage fin) - Si overfitting persistant
- max_depth (dernier recours) - Seulement si vraiment nécessaire
Approche pratique :
# Commencer simple
rf = RandomForestClassifier(n_estimators=100)
# Si plus de temps : optimiser n_estimators et max_features
param_grid = {
'n_estimators': [100, 200, 300],
'max_features': ['sqrt', 0.3, 0.5]
}
Les paramètres par défaut de scikit-learn sont excellents ! Souvent, juste augmenter n_estimators suffit.
Feature importance
https://scikit-learn.org/stable/api/sklearn.tree.html https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_classification.html#sklearn.datasets.make_classification

