Introduction au Machine Learning
Maîtriser les étapes pratiques de construction d'un modèle prédictif
Les étapes de construction d’un modèle prédictif
La regression lineaire
Fixons les idées sur un exemple simple de régression linéaire.
Voici un dataset avec 237 échantillons comprenant l’âge, le sexe, la taille et le poids d’enfants de 11,5 à 20 ans.
telecharger dataaset au format csv
Et voici en quelques lignes comment entraîner un modèle prédictif sur ces données.
Nous allons etudier comment les variables s’influencent entre elles.
A noter que
- l’âge est en mois et non en années, donc de 139 mois a 250 mois soit de 11,5 a 20 ans.
- la variable sexe est binaire: 0 pour les garçons et 1 pour les filles
- la taille en cm varie de 128.27 cm à 182.88 sm
- et la variable cible, le poids en Kg est compris entre 22.9 kg et 77.78 kg
Nous allons construire un modèle qui prédit le poids de l’enfant (la variable coble) à partir des autres variables: sexe, âge et taille, les variables dites prédictrices.
Note: nous supposons donc implictement que les variables predictrices ont une influence sur la variable cible.
On cherche donc à determiner le meilleur modele lineaire a partir des données.
Donc a trouver les coefficients a,b,c qui capturent au maximum l’information du jeux de données.
poids = a * sexe + b * age + c * taille + du bruit
où le bruit represente l’information qui n’est pas capturée par le modele linéaire.
Voici un exemple ou on ne considère que les variables de sexe et d’âge.
On charge le dataset dans une dataframe pandas
import pandas as pd
df = pd.read_csv(<le fichier csv>)
Par convention on note X la matrice des variables prédictives, aussi appelée matrice de design.
Par convention on note y le vecteur de la variable cible, aussi appelé groundtruth.
On definit la matrice de design X et le vecteur de la variable cible y.
# les variables prédictives
X = df[['age', 'taille']]
# la variable cible, le poids
y = df.poids
Maintenant, le modèle. On Choisit la régression linéaire de scikit-learn
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
Entraîner le modèle consiste à appliquer la méthode fit() sur le modèle en lui fournissant en entrée
les valeurs des variables prédictives X et de la variable cible y
reg.fit(X, y)
A ce stade le modèle est entièrement entraîné sur le jeux de donnée
Enfin, étape 3, on regarde la performance du modèle par l’intermédiaire du score
La documentation indique qu’il s’agit là du coefficient de détermination R^2
print(reg.score(X, y))
Comme il s’agit d’une régression linéaire, le modèle s’exprime
poids estimé = a * sexe + b * age + du bruit
et les coefficients a et b sont donnés par
print(reg.coef_)
ce qui dans notre cas donne
[-2.06, 0.3 ]
coefficient de détermination
Le score, coefficient de détermination, est une mesure des variations de la variable cible expliquées par le modèle.
R^2 va de 0 (mauvais) à 1 (parfait).
Info: par convention de notation on note
X, la matrice qui contient les variables prédictrices. Dans le code c’est une pandas dataframe. On appelle cette matrice la matrice de design. La matrice de design représente les données d’entrée, où chaque ligne correspond à une observation et chaque colonne correspond à une caractéristique ou variable d’entrée.y, le vecteur de la variable cible. Dans le code, c’est une série de pandas ou un array.
Maintenant, ajoutez la variable sexe à la matrice de design. et entrainez le modele.
Vous devriez observer un meilleur score que avec juste deux variables age et taille. Qu’observez vous au niveau des coefficients?
Vous pouvez enfin faire une prédiction si un nouvelle élève arrive en cours d’année: Par exemple, pour un garçon (0) agé de 150 mois et de taille 150 cm
poids = reg.predict(np.array([[0, 150, 150]]))
La fonction de coût
Dans le chapitre précédent, nous avons abordé l’exemple de l’algorithme de calcul de la racine de 2, mettant en évidence le concept d’erreur d’estimation. Cette erreur permet
- d’arrêter l’algorithme quand l’erreur atteint un certain seuil,
- mettre à jour progressivement le modèle
Le but principal d’un algorithme de machine learning est de minimiser cette erreur d’estimation. On peut estimer cet écart (données réelles - groundtruth vs données prédites) de plusieurs façons.
Au lieu de se limiter à une seule méthode de calcul, on généralise l’idée en considérant n’importe quelle fonction qui puisse servir de mesure.
On appelle ces fonctions “fonctions de coût”, où cost function en anglais.
La fonction de coût est un concept essentiel en ML. C’est une mesure de l’écart (distance) entre les prédictions du modèle et les valeurs réelles de la variable cible.
Quand dans scikit-learn (et dans d’autres librairies de ML) on applique la fonction fit() sur un modèle, on démarre l’algorithme qui va minimiser cette fonction de coût jusqu’à un atteindre un seuil minimum d’erreur.
Comme il s’agit d’une routine hautement optimisée, la fonction de coût est souvent liée au choix du modèle. Par exemple pour la régression linéaire dans scikit-learn la fonction de coût est la MSE ou Mean Squared Error définie comme suit
Evaluer la performance d’un modèle
La fonction de coût permet de faire fonctionner l’algorithme d’entraînement du modèle. Mais pour évaluer sa performance une fois entraîné, nous avons besoin de calculer un score de performance du modèle.
Ce score est une mesure de la performance du modèle sur un ensemble d’échantillons qui peut être l’ensemble de test, d’entraînement ou un autre ensemble d’échantillons. Il permet de quantifier directement la qualité des predictions du modele.
fonction de cout != metrique d’evaluation
Une même métrique peut effectivement servir à deux usages différents :
- Fonction de coût (pendant l’entraînement)
L’algorithme l’utilise pour optimiser les paramètres du modèle. C’est ce qui est minimisé (ou maximisé) pendant l’apprentissage.
- Métrique d’évaluation (après l’entraînement)
On l’utilise pour mesurer la performance du modèle sur des données de test.
Example de metriques
Conventions: dans la suite on note
X: le matrice des échantillons des variables prédictrices (colonnes).y: le vecteur de la variable cible. aussi appelé groundtruthŷ: les prédictions du modèlenest le nombre d’échantillons d’entraînement,
X est appelé la matrice de design. (c’est comme une feuille excel)
- rangées: les échantillons
- colonnes: les variables prédictrices
Examples de metriques continues frequemment utilisées
- MSE (Mean Squared Error)
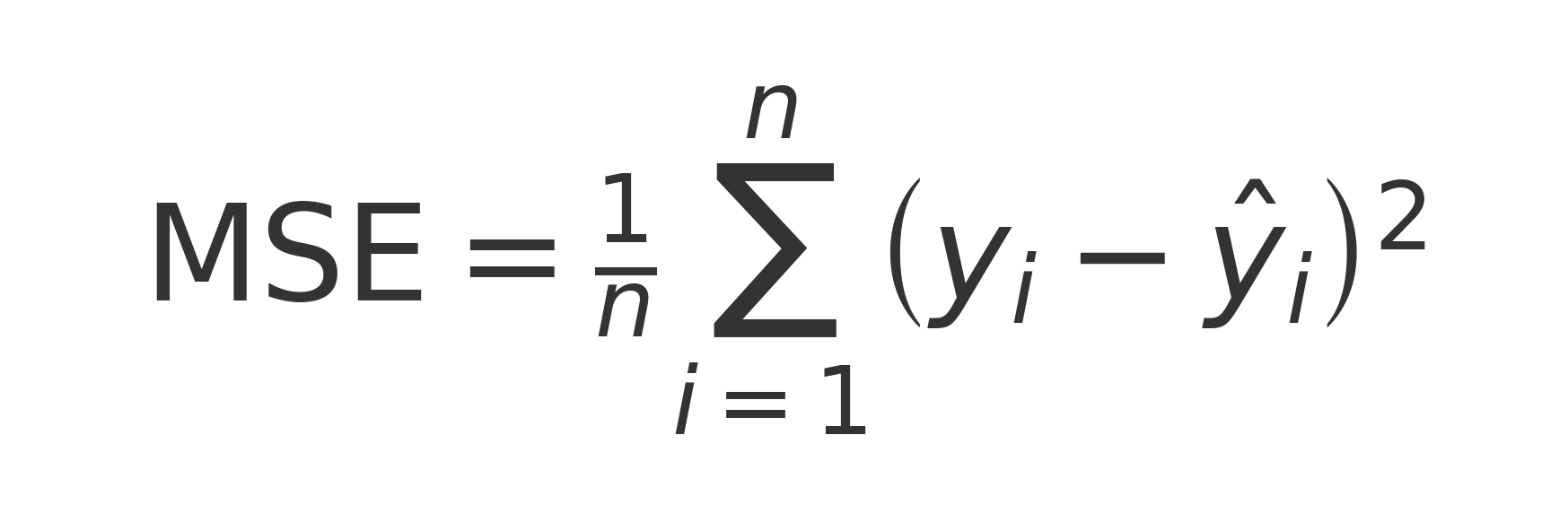
- RMSE = Root Mean Squared Error
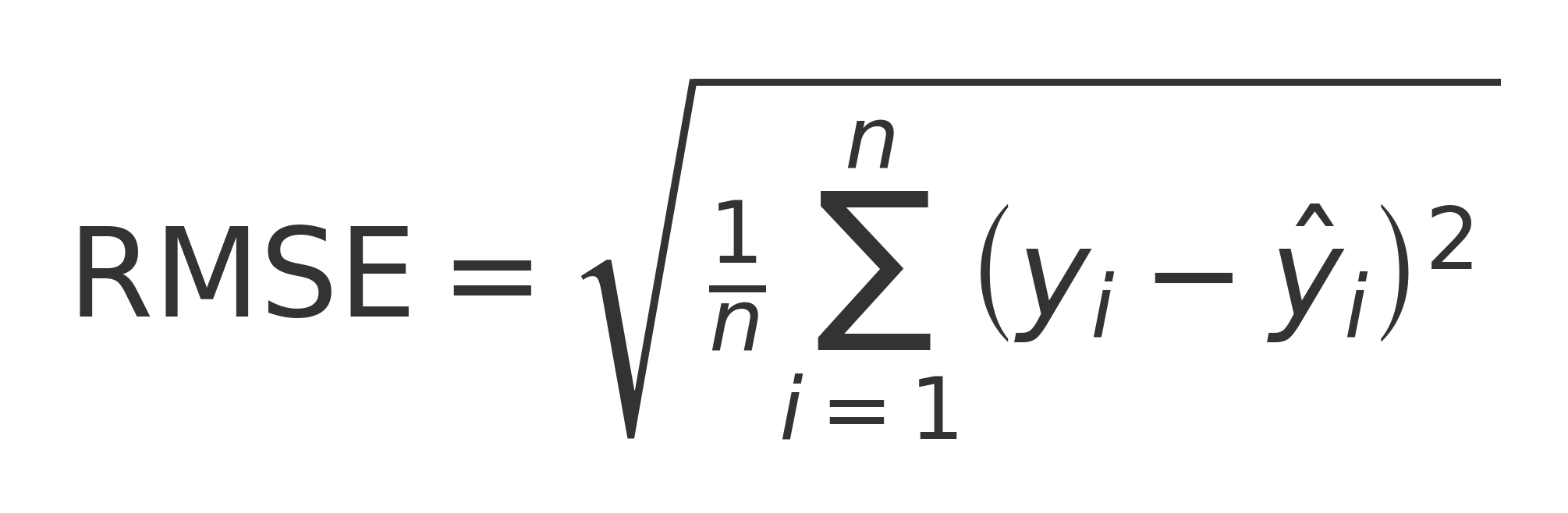
- MAPE = Mean Absolute Percentage Error
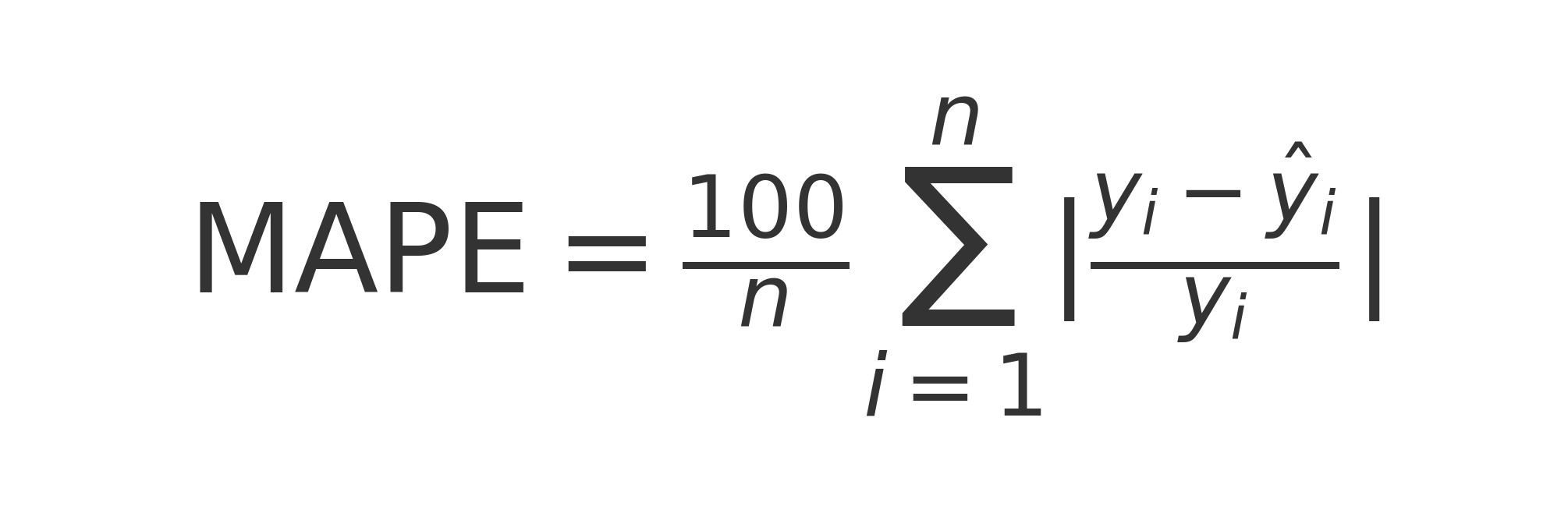
Comme la RMSE ou la MAPE sont des valeurs absolues, et non pas comprises entre 0 et 1 par ex, la comparaison entre des modèles dans des contextes différents est difficile.
On peut donc aussi considérer des variantes relatives de ces métriques ou l’on divise par la moyenne de la variable cible.
- relative RMSE
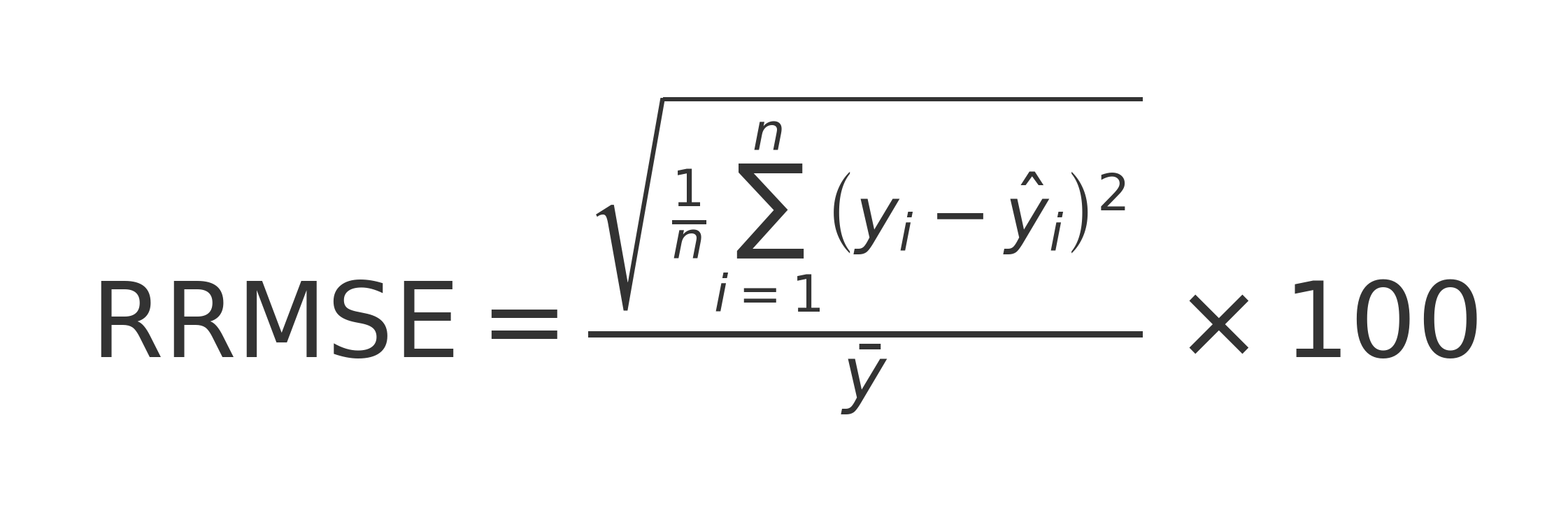
de meme on a :
- relative MAPE
- relative MAE
important: un modele performant aura une MSE (et ses variantes) proche de 0.
l’agorithme d’entrainement tente de minimiser la fonction de cout, miniser la distance entre les valeur predites et les valeurs reelles.
Le coefficient de determination R^2
Dans notre exemple précédent de regression sur le dataset enfants, age, poids, le score de performance est le R^2 aussi appelé coefficient de determination.
En voici la definition
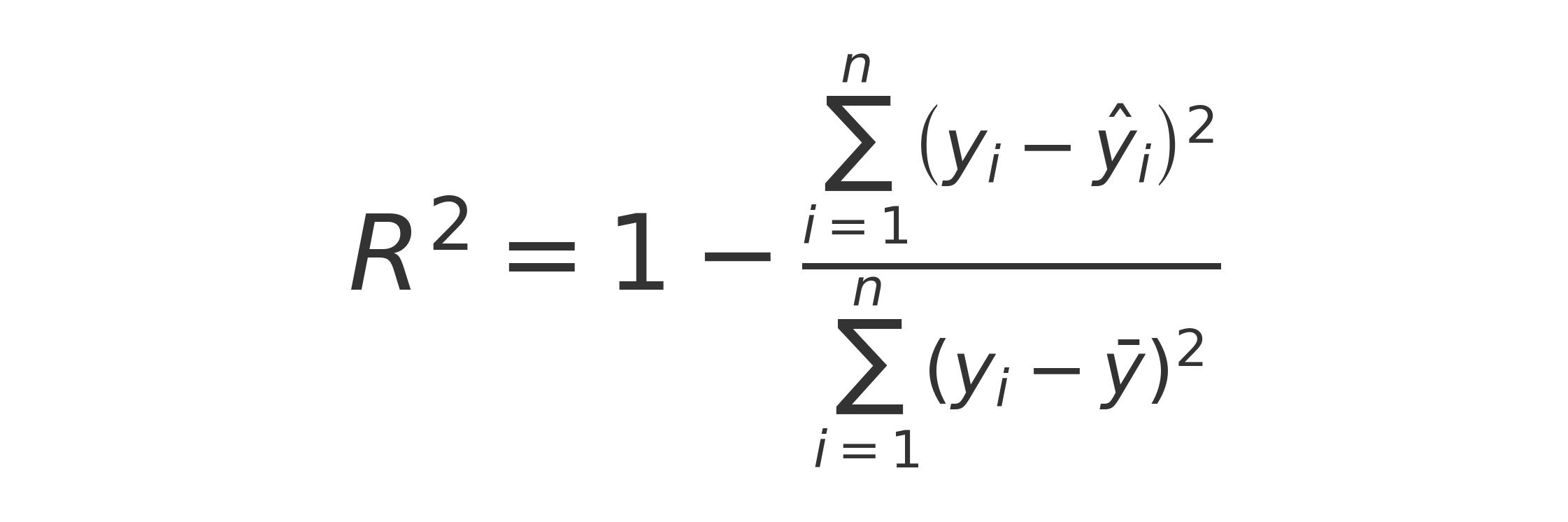
Le R^2 est une adapté a la regression lineaire.
- Métrique normalisée : entre 0 et 1 (ou négatif si très mauvais)
- Facile à interpréter : pourcentage de variance expliquée
- Permet de comparer différents modèles/datasets
Interprétation simple
Le R² représente le pourcentage de la variance de la variable cible (y) qui est expliquée par le modèle.
- R² = 0.85 → Le modèle explique 85% de la variance des données
- R² = 1 → Prédiction parfaite
- R² = 0 → Modèle pas meilleur que prédire la moyenne
- R² < 0 → Modèle pire que prédire simplement la moyenne
Autres metriques
Il existe de nombreuses metriques d’evaluation
- pas moins de 15 dans la doc sklearn pour la régression
- 16 pour le clustering
- 28 pour la classification
La méthodologie pour entrainer un modèle predictif
Avant de rentrer plus en détails dans les différences entre régression, classification et clustering, il est utile de souligner la similarité du processus d’entrainement qu’ils ont en commun.
En effet, dans ces 3 cas, entraîner un modèle predictif (ML) va consister à enchaîner ces étapes
- loader les data dans une dataframe
- améliorer (cleaning) et transformer (feature engineering) les data
- scinder les data en train / test ou train / test / validation
- entraîner le modèle avec plusieurs configurations de paramètres (quand le modèle s’y prête)
- calculer le score de chaque version du modèle pour choisir le meilleur
et recommencer pour essayer d’obtenir un meilleur score
D’autre part, le choix de la métrique de performance va influencer l’interprétation de ses performances. Nous en verrons un exemple dans le cas de la classification ou certaines métriques sont peu adaptées dans certains cas.
À vous de jouer !
Sur la documentation scikit learn:
- Montrer qu’un modèle existe le plus souvent en version régression et en version classification
- Montrer qu’il est possible de choisir parmi plusieurs métriques
Le Ridge modèle. Le modele Ridge est une generalisation de la regression lineaire.
This model solves a regression model where the loss function is the linear least squares function and regularization is given by the l2-norm.
Notez la fonction de coût
L’equivalent pour la classification est le Ridge classifier
La regression lineaire simple ou le ridge ne permettent pas de choisir la fonction de cout.
Par contre, les modeles de type arbres de décision. Dans la documentation scikit-learn, la fonction de coût est appelé le “criterion”. Remarquez qu’il y a plusieurs choix: gini, entropy, logs …
Recapitulatif
Voici un récapitulatif des points essentiels de ce chapitre :
Processus standard ML
- Conventions :
X= matrice des variables prédictives (matrice de design),y= variable cible (ground truth) - Étapes universelles : charger données → nettoyage → train/test split → entraînement → évaluation
- Méthode :
model.fit(X, y)pour entraîner,model.predict()pour prédire
Fonction de coût vs Score de performance
- Fonction de coût : mesure l’écart pendant l’entraînement (ex: MSE pour régression linéaire)
- Score de performance : évalue le modèle après entraînement (ex: R² pour régression)
- Optimisation : l’algorithme minimise la fonction de coût via descente de gradient
Métriques d’évaluation
- Régression : RMSE, MAPE, R² (coefficient de détermination : 0 = mauvais, 1 = parfait)
- Diversité : sklearn propose 15+ métriques pour régression, 28 pour classification
- Choix crucial : la métrique influence l’interprétation des performances
Réalité pratique
- Processus itératif : tester différents modèles et paramètres pour améliorer le score
- Universalité : même workflow pour régression, classification et clustering
- Versions multiples : la plupart des modèles existent en version régression et classification