Introduction au Machine Learning
Découvrir les différents types de modèles et algorithmes d'apprentissage automatique
Les modèles et les algorithmes
Découvrez les différents types de Modèles:
Nature des données et contexte: tabulaire, texte, sons, image, vidéo, séries temporelles: le ML s’applique à tout type de données => liste d’exemples. Les principaux modèles de ML: de LR (GLM) à NN/DL en passant par Tree-based; Pertinence en fonction du type et volume de données et aussi de leurs propriétés statistiques; dicte le choix des modèles et des outils. On distingue GLM,Tree et NN. Tableau comparatif.
Même si vous vous limitez au contexte supervisé tel qu’exposé au chapitre précédent, vous vous retrouverez en face d’une multitude de modèles, chacun possédant des caractéristiques propres et des performances escomptées.
La documentation de sklearn pour l’apprentissage supervisé est un bon exemple de cette richesse de choix. https://scikit-learn.org/stable/supervised_learning.html#supervised-learning
Ne pouvant tous les tester un par un, vous aller donc devoir choisir rapidement comment vous équiper pour la tâche à venir.
En règle générale, vous choisirez le modèle en fonction du contexte et du cahier des charges.
- la tâche à effectuer: régression, classification ou clustering
- la nature des données: chiffres, catégories, texte, images, vidéo, sons, séries temporelles
- le nombre d’échantillons, du volume des données
Le schéma suivant est extrait de la documentation de scikit-learn. Bien qu’un peu daté, il résume le processus de choix d’un modele.
Cependant, pour vous faire gagner du temps, on distingue après 2020:
-
les modèles de régression: adaptés à des jeux de données de taille limitée ou les relations entre les variables sont supposées être linéaire jusqu’à un certain point. On parle aussi de Generalized Linear Model (GLM), famille de modèle qui comprend les différents types de regression linéaire.
-
les modèles à base d’arbres: decision tree, random forest, ainsi que XGBoost et ses nombreuses variantes. Ces modèles sont adaptés à des jeux de données plus conséquent, capable de prendre en compte tout types de données: catégorie et robuste face au outliers et données manquantes. Ce sont de loin les modèles les plus utilisés sur des jeux de données de taille raisonnable. Grand gagnants des récentes compétitions Kaggle.
-
enfin, les réseaux de neurone et le deep learning, adaptés à des jeux de donnée de gros volume, de nature plus complexes comme des images ou de la video.
Les autres types de modèles bien qu’adaptés dans certains contexte, n’offriront pas la versatilité et la robustesse ce cette short liste. Ils sont devenu obsoletes alors que d’autres emergeaient comme plus puissant. C’est le cas par exemples des SVMs, elegants mathematiquement mais peu competitifs face a XGBoost.
Depuis quelques années, XGBoost est le grand vainqueur des compétitions Kaggle et des concours de modélisation. C’est un modèle qui a fait ses preuves.
Sachez définir un modèle
Fixer les idées: Modélisation ou modèle. distinguer le type de modèle du modèle entraîné sur un jeu de donnée particulier dans un but particulier. parallèle avec la classe et l’instance en programmation.
Mais qu’est ce qu’un modele de Machine learning ? De quoi parle-t on au final quand on parle de modele ?
On va distinguer
- le type de modele: XGBoost, reseaux de neurones, regression lineaire: il s’agit la de la methode issue d’un raisonnement mathematique et traduite en code.
En python on importe le modele
from sklearn.ensemble import RandomForestClassifier
- et son instanciation lors de l’entrainement du modèle sur les données. On utilisera cette instance du modèle pour effectuer des prédictions sur de nouveaux échantillons
En python cela consiste à utiliser la methode fit. Par exemple:
from sklearn.ensemble import RandomForestClassifier
X = [[0, 0], [1, 1]]
Y = [0, 1]
clf = RandomForestClassifier(n_estimators=10)
clf = clf.fit(X, Y)
dans ce code, clf est le modele entraîné sur les données X et Y. RandomForestClassifier est le type de modèle.
Par soucis de simplcité on parle dans les 2 cas du modèle.
Sachez définir un algorithme
Définir ce qu’est un algo, illustrer avec l’algo pour calculer
\sqrt(2). donner le code. Faire le lien avec le ML; mentionner le gradient stochastique
Nous avons donc un modele entrainé sur des données. Mais comment se passe cette entrainement ?
Nous ne rentrerons pas ici dans le arcanes des algorithmes d’entrainement, procédures ultra-optimisées en C, cela serait hors sujet pour ce cours. Mais je voudrais illustrer par un exemple, ce qu’est un algorithme. Ce quipermettra de faire jaillir une notion fondamentale du machine learning: l’erreur d’estimation!
La définition officielle d’uin algorithme: Un algorithme est une série d’instruction définies et ordonnées qui permettent d’effectuer une tâche spécifique, un calcul par exemple.
Prenons donc un exemple simple avec le calcul de la racine de 2. Sans utiliser une calculatrice, nous pouvons calculer la racine de 2 par une série de calculs plus simples.
On aboutit en quelqeus itérations à une bonne approximation du résultat escompté.
Pour cela, nous allons utiliser la méthode de Héron dite méthode babylonienne, inventée au 1er siècle apres JC par les babyloniens. La science des algorithmes ne date pas d’hier. Excellente méthode efficace d’extraction de racine carrée (ou plus d’ailleurs)!
Partons d’une valeur candidate (x = 1) et mettons à jour cette valeur jusqu’a ce que le résultat soit assez proche du résultat attendu. On saura simplement si x est proche de la racine carrée de 2 si x^2 est proche de 2.
Voici donc l’agorithme de Héron pour le calcul des racines carrées
- soit une valeur d’initialisation pour x:
x = 1 - fixons la precision attendue:
precision = 0.001
Tant que |x^2 - 2| > precision :
x = (x + 2/x)/2
En python, cela s’ecrit
x = 1
precision = 0.001
while (abs(x**2 - 2) > precision) :
x = (x + 2/x)/2
print(x)
Cet algorithme est extrêmenent efficace. En seulement trois étapes, la précision relative sur la valeur de √2 est déjà de 10–6, ce qui est excellent, et de moins de 10^{–12} en quatre étapes.
Remarquez maintenant la quantite |x^2 - 2| que nous avons calculé à chaque itération: la différence en valeur absolu entre la valeur candidate au carré et 2. C’est l’erreur d’estimation entre la valeur candidate, notre valeur estimée et la valeur dite de vérité (groundtruth en anglais)
On peut réecrire l’algo en mettant en avant cette erreur d’estimation
x = 1
erreur = 1
precision = 0.001
Tant que erreur > precision:
# maj de l'estimation
x = (x + 2/x)/2
# maj de l'erreur avec la nouvelle valeur de x
erreur = |x^2 - 2|
soit en python
x = 1
error = 1
precision = 0.001
while error > precision:
# Update the estimation
x = (x + 2/x) / 2
# Update the error with the new value of x
error = abs(x**2 - 2)
print(f"Approximation of √2: {x}")
print(f"Final error: {error}")
print(f"Actual √2: {2**0.5}")
print(f"Difference: {abs(x - 2**0.5)}")
Voila, dans ce simple algorithme qui date de 2000 ans, nous avons les composantes principales d’un algorithme de machine learning
- la notion d’erreur d’estimation:
erreur = |x^2 - 2| - la mise a jour itérative de l’estimation:
x = (x + 2/x)/2
Note: au lieu de calculer la valeur absolu de l’erreur d’estimation, nous aurions put aussi prendre son carrée
Dans ce cas, nous aurions eu l’algorithme suivant
Tant que erreur > precision:
# maj de l'estimation
x = (x + 2/x)/2
# maj de l'erreur avec la nouvelle valeur de x
erreur = (x^2 - 2)^2
La question est alors de savoir si ce critère fait converger plus ou moins rapidement l’estimation de la racine de 2. Qu’en pensez vous?
gradient stochastique
Le principal algorithme qui sert à entrainer la plupart des modèles de ML, deep learning inclus, s’appelle le gradient stochastique. Sans rentrer dans les details, le GS fonctionne comme l’algo de Héron .
Soit un jeux d’echantillons. On cherche a estimer un vecteur h qui minimise un critère, une fonction de coût.
On se dote d’un paramètre essentiel, le learning rate souvent noté \alpha et aussi appelé taux d’apprentissage, qui va permettre d’adapter la correction de l’estimation en fonction de l’erreur d’estimation.
On aura de façon simplifié à chaque itération:
calcul de l'erreur = f(estimation)
maj de l'estimation = estimation * \alpha * f(erreur)
stop en fonction de l'erreur
En pratique, étant donné un jeu de donné, cela donne:
- Phase d’initialisation du vecteur h, par exemple que des zeros
- A chaque itération
- sélectionner les échantillons (aléatoire ou sous-échantillonage)
- calculer l’erreur d’estimation:
een fonction deh:e = f(h) - maj de
hen fonction de l’erreure:h = h + \alpha * e
En pratique, le parametre \alpha sert à regler la rapidite de convergence de l’algorithme et la precision des resultats. C’est le taux d’apprentissage / learning rate.
alphapetit: convergence lente mais meilleure precisionalphagrand: convergence rapide mais resultat moins precisalphatrop grand: explosion et non convergence.
C’est un des parametres principal des modeles que vous serez amené a entrainer.
Mise en pratique
Illustration de l’influence du learning rate sur la vitesse de convergence
Tout d’abord importer les librairies python
import matplotlib.pyplot as plt
import numpy as np
import math
Voici une definition complete de la function de l’algorithme appelé Newton-Raphson
La fonction retourne la series de erreurs successives en log.
def sqrt2(x, error, precision, learning_rate):
"""
Calculate square root of 2 using Newton-Raphson method with learning rate.
Logs the natural logarithm of error values at each iteration.
Parameters:
x (float): Initial estimation
error (float): Initial error value
precision (float): Precision threshold to stop iteration
learning_rate (float): Learning rate to control update step
Returns:
list: log(error) values at each iteration
"""
log_errors = []
iterations = 0
while error > precision:
# Calculate the Newton-Raphson update
x_new = (x + 2/x) / 2
# Apply learning rate to control the update step
x = x + learning_rate * (x_new - x)
# Update the error with the new value of x
error = abs(x**2 - 2)
log_errors.append(math.log(error))
iterations += 1
if iterations > 10000: # safety check
print("Warning: Maximum iterations reached")
break
return log_errors
On peut ensuite jouer avec differentes valeur de learning rate
# Define a colorblind-friendly colormap
colors = plt.cm.viridis(np.linspace(0, 1, len([0.001, 0.01, 0.1, 0.5])))
for i, lr in enumerate([0.001 0.01, 0.1, 0.5]):
err = sqrt2(1, 1, 0.001, lr)
plt.plot(err, label=f'LR = {lr}, nitr ={len(err)} ', color=colors[i])
plt.xlabel('Iterations')
plt.ylabel('log(Error)')
plt.title('Convergence of sqrt(2) using Newton-Raphson with different Learning Rates')
plt.legend()
plt.grid(True)
plt.show()
Cela donne la figure suivante
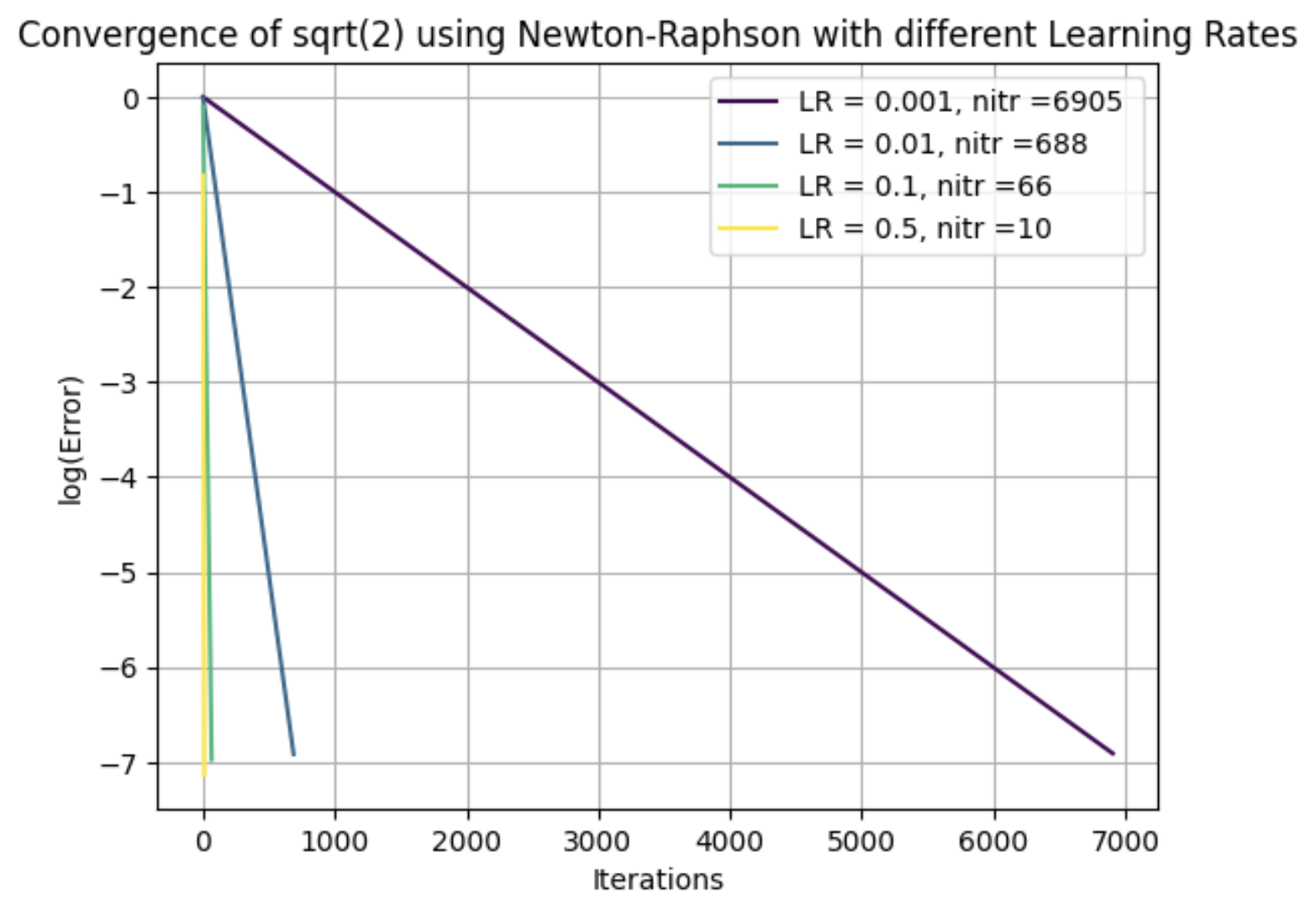
ou nitr correspond au nombre d’itération nécessaire pour converger, atteindre la précision souhaitée.
ce qu’il faut retenir:
Accroitre la valeur du learning rate permet de converger plus vite
Recapitulatif
Voici un récapitulatif des points clés de ce chapitre sur les modèles et algorithmes :
Classification des modèles ML
- Modèles de régression (GLM) : adaptés aux données de taille limitée avec relations linéaires, famille des modèles linéaires généralisés
- Modèles à base d’arbres : Decision Tree, Random Forest, XGBoost - les plus performants sur données tabulaires, robustes aux outliers et données manquantes
- Réseaux de neurones (Deep Learning) : pour gros volumes de données complexes (images, vidéo, audio)
Distinction modèle vs instance
- Type de modèle : la méthode mathématique traduite en code (ex:
RandomForestClassifier) - Modèle entraînée : le modèle entrainé sur des données spécifiques, prêt pour les prédictions
Concepts algorithmiques fondamentaux
- Algorithme : série d’instructions ordonnées pour accomplir une tâche (ex: méthode de Héron pour √2)
- Erreur d’estimation : différence entre valeur estimée et valeur de vérité (
|x² - 2|) groundtruth - Mise à jour itérative : amélioration progressive de l’estimation à chaque étape
Gradient stochastique - moteur du ML
- Algorithme principal pour entraîner la plupart des modèles ML
- Learning rate (α) : paramètre contrôlant la qauntité de mise à jour de l’estimation et donc la vitesse de convergence
- Principe :
estimation = estimation + α × erreur
Règle pratique
- XGBoost : grand vainqueur des compétitions Kaggle, modèle de référence pour données tabulaires
- Trade-off : learning rate élevé → convergence rapide mais moins précise