Introduction au Machine Learning
Apprendre à entraîner un modèle de régression linéaire
La régression linéaire
La régression linéaire est le modèle le plus simple pour modéliser et prédire des valeurs continues en fonction d’autres variables. Mais c’est une méthode extrêmement puissante.
Pensez-y comme une ligne droite qui relie les points dans un nuage de données, captant ainsi la tendance générale des observations.
=> illustration
De façon plus rigoureuse, lorsque l’on prédit une variable y à partir d’une variable x, la régression linéaire consiste a trouver les coefficients a et b dans l’équation de la droite
y = a x + b.
Dans le cas de 2 variables de prédictions x_1 et x_2 de y, le modèle correspond à l’équation du plan défini par
y = a x_1 + b x_2 + c
De façon générale, si on a N variables {x_1, …, x_N} de prédictions dans notre dataset pour la prédiction d’une variable y le modèle de récession linéaire consiste à trouver les N coefficients c_1, … c_N de l’équation:
y = c_1 x_1 +_ c_2 x_2 + ... + c_N x_N + c_{N+1}
De façon abrégée nous écrirons:
y ~ x_1 + x_2 + + x_N
Notez le signe ~ qui veut dire que l’on régresse la variable cible y par rapport aux variables de prédictions x_1, …, x_N
Vocabulaire
La régression linéaire est utilisé dans de nombreux domaines comme la médecine, l’économie, etc et chacun de ces domaine utilise un vocabulaire différent pour désigner les variables cibles et les variables de prédictions.
Vous trouverez donc les équivalents suivants
- variable cible: variable dépendante ou endogène. C’est la variable à expliquer, à prédire.
y - variables de prédictions: variables d’entrée ou indépendantes ou exogènes. Ce sont les variables d’entrée du modèle à partir desquelles on va prédire la variable cible.
X
Je trouve la distinction entre dépendante et indépendante peu parlante et dans ce cours nous utiliserons les termes de:
- variable cible
- variables de prédictions ou variables d’entrées
Pourquoi utiliser la regression lineaire?
La simplicité de la régression linéaire lui confère des propriétés précieuses:
- interprétabilité: le poid respectif des coefficients montre le poids relatif des variables dans la prédiction
- facilité d’implémentation: en tout langage, dans toutes les librairies
- rapidité de calcul: optimisée depuis des lustres les calculs sont hyper rapides
- consomme peu de mémoire: étant hyper optimisé depuis longtemps
La régression linéaire a de beaux jours devant elle.
A noter que la régression linéaire est d’avantage un outil de modélisation statistique que de machine learning. Il est possible de réaliser des analyses poussées de données avec des librairies comme statsmodels en python ou lm en R.
Ici, nous utiliserons d’abord la régression linéaire pour sa simplicité avant de passer à des modèles de ML plus puissants.
Les limites de la régression linéaire
Utiliser une régression linéaire nécessite cependant de prendre quelques précautions.
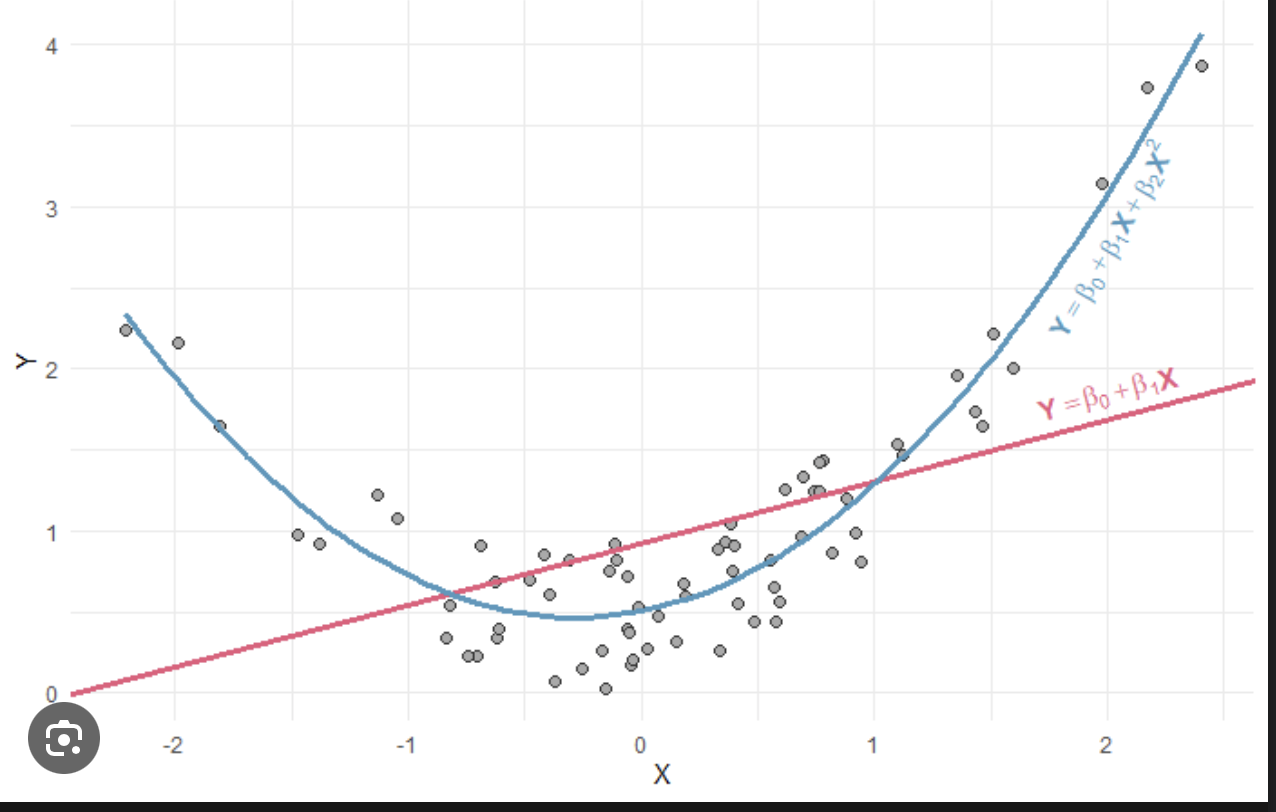
En effet, il est nécessaire pour que le modèle ait une quelconque valeur que la relation entre la variable cible et les prédicteurs soit … linéaire. Utiliser une LR dans des cas évidemment non linéaires ne marchera pas.
non linéaire vs linéaire
Mais qu’est ce qu’un cas non linéaire?
Supposons que nous ayons un jeu de données de la croissance d’une plante en fonction de la quantité de lumière qu’elle reçoit. Si nous traitons un graphique de ces données, on observe que la relation entre la croissance de la plante et la lumière est en forme de U inversé.
Lorsque l’on trace la droite résultant de la régression linéaire, on voit bien que celle-ci n’explique en rien la courbe de croissance de la plante.
Supposons par contre que nous ayons un jeu de données du prix d’appartements en fonction de leur superficie en mètres carrés dans une ville donnée. la ligne de régression sera plus à même de fournir une estimation raisonnable d’un appartement dont on ne connaît que la superficie
normalisation des variables
Une autre précaution utile consiste à vérifier l’amplitude des valeurs des variables.
En effet, les valeurs des coefficients de la régression linéaire est inversement proportionnelle à l’amplitude de la variable associée.
Si une variable est 1000 fois plus grande en moyenne qu’une autre variable, et si ces 2 variables ont le pouvoir de prédiction sur la variable cible, alors le coefficient de la grande variable sera 1000 fois plus petit que celui de la deuxième variable.
Prenons par exemple un dataset avec deux prédicteurs : x_1 (coefficient c_1) dont les valeurs vont de 1 à 10, et x_2 (coefficient c_2) dont les valeurs vont de 1 à 1000. Dans ce cas, le coefficient c_2 sera beaucoup plus petit que c_1, même si x_2 a un impact plus important sur la variable cible que x_1.
Il est donc essentiel de normaliser les variables car des variations d’amplitude significatives peuvent fausser l’importance des coefficients et impacter les prédictions du modèle.
Si les variables sont normalisées de façon à ce que leurs amplitudes soient toutes comprises entre 0 et 1 (ou dans un intervalle comparable) alors la valeur de chaque coefficient de la régression linéaire peut etre interpreter comme etant l’impact de la variable sur la variable cible
Let’s regress
Considérons un nouveau dataset intitulé advertising disponible ici
C’est un dataset classique issu du livre référence An introduction to statistical learning.
Il contient 200 échantillons, sur le budget alloué aux publicités télévisées, à la radio et dans les journaux, ainsi que les ventes qui en résultent.
- Variable cible: Ventes (sales dans la version originale)
Variables predictions
- TV - Budget de publicité pour la TV
- Radio - Budget de publicité pour la radio
- Journaux - Budget de publicité pour la presse (newspaper dans la version originale)
Si vous n’avez pas lu un journal depuis longtemps, que vous avez perdu la télécommande de votre télévision et que la radio c’est seulement dans la voiture, vous pouvez remplacer les intitulés des variables TV, Radio et Journaux par Facebook, TikTok et Youtube. ;)
La variable cible, ventes ou sales, est continue, donc nous sommes dans une logique de régression (et non de classification).
Nous allons essayer de prédire le volume de vente en fonction du budget publicitaire en TV, Radio, et Journaux.
Chargeons et explorons le dataset.
import pandas as pd
df = pd.read_csv("advertising.csv")
df.head()
df.describe()
df.info()
Avant d’entraîner le modèle, il convient de tracer les relations entre les différentes variables.
Pour cela nous utilisons seaborn et matplotlib, les principales librairies de visualisation data en python
La fonction regplot() de seaborn permet non seulement d’afficher le nuage de point des variables tv, radio et journaux en fonction des ventes mais aussi de tracer la ligne de régression. La zone grisée reflète l’incertitude du modèle. Plus elle est grande, moins la régression est fiable.
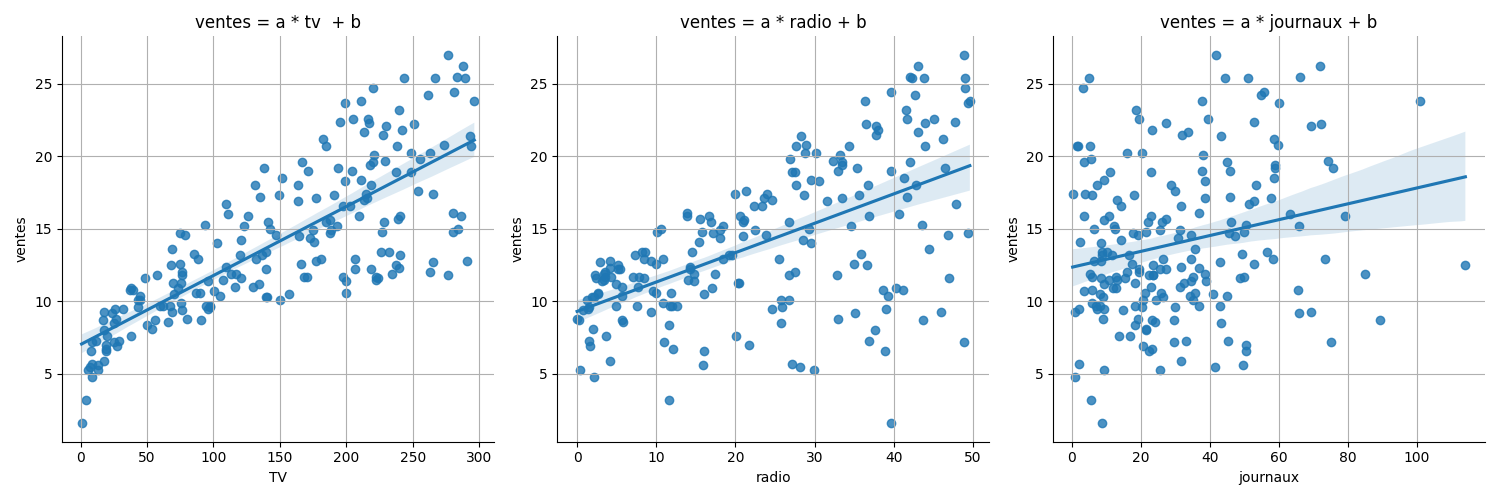
On remarque que la variable tv est plus liée à la variable radio qui elle même est plus liée à la variable journaux.
C’est confirmé par les coefficients de corrélation entre ces variables et la variable ventes
df.corr()
- tv 0.78
- radio 0.58
- journaux 0.23
Choisissons le modèle de régression linéaire de scikit-learn
# on choisit un modèle de régression linéaire
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
Cette fois-ci, on va scinder notre dataset en une partie d’entraînement du modèle et une parti d’évaluation en utilisant la fonction train_test_split de scikit-learn https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
Cette fonction prends les variable d’entrées, la variable cible, un ratio et retourne 4 objets
- X_train: les variables d’entrée pour le sous-ensemble d’entraînement
- X_test: les variables d’entrée pour le sous-ensemble d’évaluation
- y_train: la variable cible pour le sous-ensemble d’entraînement
- y_test: la variable pour le sous-ensemble d’évaluation
On va ensuite utiliser X_train et y_train pour entraîner le modèle et X_test, y_test pour l’évaluer.
Cela donne
from sklearn.model_selection import train_test_split
X = df[['tv','radio','journaux']]
y = df.ventes
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=42)
comme notre jeux de données a 200 échantillons et que l’on en réserve 20% pour le test on aura les tailles suivantes (X.shape et y.shape) :
- X_train: 160 * 3
- X_test: 40 * 3
- y_train: 160 * 1
- y_test: 40 * 1
On a donc 160 échantillons pour entraîner notre modèle et 40 échantillons que le modèle n’aura pas vu pendant son entraînement et qui nous serviront à l’évaluer.
Le terme “random_state” est un paramètre qui permet de contrôler la reproductibilité des résultats lorsque vous effectuez des opérations qui impliquent de l’aléatoire comme par exemple de scinder les données en sous-ensemble de test et de train. En fixant une valeur spécifique pour “random_state”, par exemple 42 comme dans l’exemple ci-dessus, vous vous assurez que les opérations aléatoires se déroulent toujours de la même manière lorsque vous exécutez votre code avec les mêmes données. Les résultats sont reproductibles et vous pouvez comparer différents modèles entraînés.
Let’s go!
On entraîne le modèle avec la fonction fit()
reg.fit(X_train, y_train)
Pour estimer la performance sur le sous-ensemble de test il faut tout d’abord obtenir les prédictions pour X_test
cela donne
y_hat_test = reg.predict(X_test)
(on note avec un “_hat” tout ce qui relève des prédictions du modèle)
On peut maintenant calculer l’écart entre les vraies valeurs de test (y_test) et celles prédites par le modèle.
Utilisons la RMSE et la MAPE comme score. Pour ces 2 métriques, un score plus petit correspond à un meilleur modèle. MAPE est compris entre 0 et 1, tandis que RMSE n’est pas contraint.
from sklearn.metrics import mean_squared_error print(f”RMSE: {mean_squared_error(y_test, y_hat_test)}”)
On obtient
- RMSE: 3.17
- MAPE: 0.15
Est- ce bien ? Est-ce un mauvais score ? Difficile de dire comme la RMSE n’est pas absolue. Une MAPE de 0.15 semble bien, plutôt à gauche de l’intervalle [0,1].
Mais peut-on faire mieux?
Ayant lu le livre mentionné au début du chapitre, je sais déjà quelles améliorations apporter à cette première régression linéaire. Je vais donc tricher et vous proposer directement les 2 améliorations qui marchent.
- Première amélioration: Ajouter un terme quadratique
ok, quadratique veut simplement dire “au carré”
Si l’on regarde bien le scatterplot (nuage de point) de ventes par rapport à tv, on remarque que ce nuage de point suit plutôt une courbe qu’une ligne droite. C’est particulièrement vrai pour la partie gauche du graphe.
=> illustration
On peut en déduire que la relation entre ventes et tv n’est pas simplement linéaire
cad ventes = a * tv + b
mais dépend aussi d’un terme tv^2 comme ceci
ventes = a * tv + b * tv^2 + c
c’est un polynôme du second degré.
Lorsqu’on ajoute une puissance de l’une des variables dans la régression, on fait ce qu’on appelle une régression polynomiale
encart régression: polynomiale La régression polynomiale consiste à ajouter les puissances de certains prédicteurs dans la régression. C’est une façon simple pour capturer les relations non linéaires entre les données.
Note sur l’amplitude des variables: Avant d’entraîner ce nouveau modèle, on remarque que l’amplitude des variables tv, radio, journaux et surtout tv^2 va être très variable.
Il va nous falloir tout d’abord normaliser ces variables, pour que leur amplitudes soient toutes comprises entre 0 et 1
Note: il y a plusieurs façons de normaliser ou standardiser des variables. Scikit-learn offre différentes méthodes pour cela https://scikit-learn.org/stable/modules/classes.html#module-sklearn.preprocessing
Nous utiliserons le MinMaxScaler qui force les valeurs des variables entre 0 et 1.
Donc:
on crée la nouvelle variable tv2 = tv^2
df[‘tv2’] = df.tv**2
et on normalise en utilisant le MinMaxScaler
Dans sklearn, appliquer un “Scaler”, consiste à 1.l’importer
from sklearn.preprocessing import MinMaxScaler
- le créer (l’instantialiser)
scaler = MinMaxScaler()
- le fit sur les données (le scaler calcule alors les min et max des variables )
scaler.fit(df)
- et enfin transformer les données
df = scaler.transform(df)
Les étapes 3 et 4 peuvent être concentrées en utilisant la méthode fit_transform(), ce qui donne en tout
from sklearn.preprocessing import MinMaxScaler scaler = MinMaxScaler() df = scaler.fit_transform(df)
À ce stade, df ne contient que des valeurs entre 0 et 1
print(df.describe())
Voici maintenant la matrice de design ainsi que le groundtruth
X = df[[‘tv’,’radio’,’journaux’, ‘tv2’]] y = df.ventes
Entraînons maintenant notre nouvelle régression linéaire que l’on peut maintenant qualifier de régression polynomiale grâce à la présence du terme quadratique tv2
y ~ tv + radio + journaux + tv2
Le python :
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=42)
reg.fit(X_train, y_train) y_hat_test = reg.predict(X_test)
print(f”Coefficients: {reg.coef_}”) print(f”RMSE: {mean_squared_error(y_test, y_hat_test)}”) print(f”MAPE: {mean_absolute_percentage_error(y_test, y_hat_test)}”)
ce qui donne: …
On note une nette amélioration par rapport au premier modèle.
On peut voir l’impact du terme en tv2 en regardant les coefficients: …
Mais on peut encore faire mieux! Il se trouve que dépenser pour la tv et la radio en même temps accroît encore plus les ventes que si on dépense uniquement sur la tv ou la radio. (c’est dans le livre). Ce qui est s’exprime par un nouveau terme croisé tv * radio
Entraînons donc un 3eme modele de regression
y ~ tv + radio + journaux + tv*radio
le python:
df[‘tv_radio’]= df.tv * df.radio
X = df[[‘tv’,’radio’,’journaux’, ‘tv_radio’]] y = df.ventes X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=42)
reg.fit(X_train, y_train) y_hat_test = reg.predict(X_test)
print(reg.coef_) print(f”RMSE: {mean_squared_error(y_test, y_hat_test)}”) print(f”MAPE: {mean_absolute_percentage_error(y_test, y_hat_test)}”)
Et on a encore un meilleur score pour le RMSE et la MAPE!!
A ce stade on a exploité toute l’information possible du dataset
À vous de jouer !
On a parlé du paramètre random_state qui permet de contrôler l’aspect aléatoire du “train, test, split”.
En faisant varier ce paramètre, les données seront réparties parmi les sous-ensembles entraînement et test de façon différente et par conséquent le modèle ne sera pas entraîné sur les mêmes échantillons.
Dans le dataset advertising cela ne posera pas de problème et vous allez vous en assurer car il n’y a pas d’échantillons avec des valeurs extrêmes (outliers).
Cependant imaginez que parmi le jeu de données se trouve quelques échantillons très différent des autres. Par exemple, un très fort budget en journaux (> 200 par exemple). Si ces échantillons se retrouvent dans le sous-ensemble d’entraînement, le modèle va le prendre en compte et la droite de régression sera plus plate que si ces échantillons se trouvaient dans le sous-ensemble de test.
=> illustration
En général, et nous verrons cela dans un prochain chapitre, il faut donc considérer plusieurs séparations en train et test pour valider que le modèle soit réellement robuste.
A vous de jouer
-
reprenez les exemples de modèles de ce chapitre et modifiez simplement la valeur du random_state
-
comparez les différents scores
-
vous pouvez en même temps jouer sur le ratio de répartition entrainement / test test_size
Si par exemple vous augmentez test_size fortement, par exemple test_size = 0.80, le modèle aura très peu d’échantillons pour s’entraîner et sera plus sensible à la répartition des échantillons entre le test et le train.
Pour voir cet effet,
- augmentez test_size =0.8 (seulement 20% des échantillons serviront à entraîner le modèle)
- testez la régression pour différentes valeurs de random_state
Les scores devraient varier bien plus en fonction des valeurs de random_state que pour un test_size de 0.2